
【題目】如圖,AB為⊙O的直徑,點P在AB的延長線上,點C在⊙O上,且PC2=PBPA.
(1)求證:PC是⊙O的切線;
(2)已知PC=20,PB=10,點D是![]() 的中點,DE⊥AC,垂足為E,DE交AB于點F,求EF的長.
的中點,DE⊥AC,垂足為E,DE交AB于點F,求EF的長.
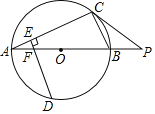
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)連接OC,證明△PBC∽△PCA,得到∠PCB=∠PAC,根據直徑得到∠ACB=90°,再利用OC=OB推導出∠PCB+∠OCB=90°即可得到結論;
(2)連接OD,根據PC2=PBPA求出AB=30,設BC=x在Rt△ABC中根據勾股定理求出x,證明△DOF∽△ACB求出![]() ,根據EF∥BC得到
,根據EF∥BC得到![]() ,由此求出EF.
,由此求出EF.
(1)證明:連接OC,如圖1所示:
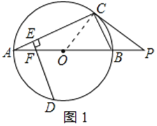
∵PC2=PBPA,即![]() ,且∠P=∠P,
,且∠P=∠P,
∴△PBC∽△PCA,
∴∠PCB=∠PAC,
∵AB為⊙O的直徑,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵OC=OB,
∴∠OBC=∠OCB,
∴∠PCB+∠OCB=90°,即OC⊥PC,
∴PC是⊙O的切線;
(2)解:連接OD,如圖2所示:
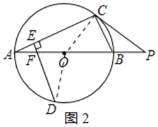
∵PC=20,PB=10,PC2=PBPA,
![]() ,
,
∴AB=PA﹣PB=30,
∵△PBC∽△PCA,
∴![]() ,
,
設BC=x,則AC=2x,在Rt△ABC中,x2+(2x)2=302,
解得:![]() ,即BC=
,即BC=![]() ,
,
∵點D是![]() 的中點,AB為⊙O的直徑,
的中點,AB為⊙O的直徑,
∴∠AOD=90°,
∵DE⊥AC,
∴∠AEF=90°,
∵∠ACB=90°,
∴DE∥BC,
∴∠DFO=∠ABC,
∴△DOF∽△ACB,
∴![]() ,
,
![]() ,即
,即![]() ,
,
∵EF∥BC,
∴![]() ,
,
![]() .
.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,AC是⊙O的一條弦,D為弧BC的中點,作DE⊥AC,垂足為AC的延長線上的點E,連接DA,DB.
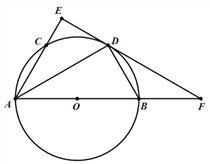
(1)求證:DE為⊙O的切線;
(2)試探究線段AB,BD,CE之間的數量關系,并說明理由;
(3)延長ED交AB的延長線于F,若AD=DF,DE=![]() ,求⊙O的半徑;
,求⊙O的半徑;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(新知探究)新定義:平面內兩定點 A, B ,所有滿足![]() k ( k 為定值)的 P 點形成的圖形是圓,我們把這種圓稱之為“阿氏圓”,
k ( k 為定值)的 P 點形成的圖形是圓,我們把這種圓稱之為“阿氏圓”,
(問題解決)如圖,在ABC 中,CB 4 , AB 2AC ,則ABC 面積的最大值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解我市九年級學生身體素質情況,從全市九年級學生中隨機抽取了部分學生進行了一次體育考試科目測試(把測試結果分為四個等級:A級:優秀;B級:良好;C級:及格;D級:不及格),并將測試結果繪成了如下兩幅不完整的統計圖.請根據統計圖中的信息解答下列問題:
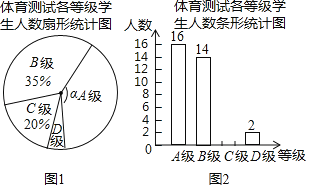
(1)本次抽樣測試的學生人數是 ;
(2)圖1中∠α的度數是 °,把圖2條形統計圖補充完整;
(3)全市九年級有學生6200名,如果全部參加這次體育科目測試,請估計不及格的人數為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有一列數a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=-2018,a98=-1,且滿足任意相鄰三個數的和為常數,則a1+a2+a3+…+a98+a99+a100的值為( )
A.1985B.-1985C.2019D.-2019
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校1000名學生一周在校參加體育鍛煉的時間,現從各年級隨機抽取了部分學生,對他們一周在校參加體育鍛煉的時間進行了調查,并繪制出如下的統計圖①和圖②,根據相關信息,解答下列問題:
(Ⅰ)本次接受隨機抽樣調查的學生人數為 ,圖①中![]() 的值為 ;
的值為 ;
(Ⅱ)求本次調查獲取的樣本數據的平均數、眾數和中位數;
(Ⅲ)根據樣本數據,估計該校一周在校參加體育鍛煉的時間大于![]() 的學生人數.
的學生人數.
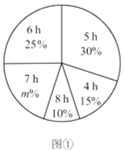
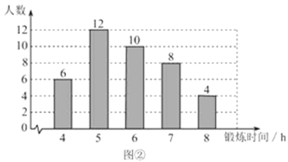
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七年級同學最喜歡看哪一類課外書?某校隨機抽取七年級部分同學對此進行問卷調査(每人只選擇一種最喜歡的書籍類型).如圖是根據調查結果繪制的兩幅統計圖(不完整).請根據統計圖信息,解答下列問題:

(1)一共有多少名學生參與了本次問卷調查;
(2)補全條形統計圖,并求出扇形統計圖中“其他”所在扇形的圓心角度數;
(3)若該年級有400名學生,請你估計該年級喜歡“科普常識”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() ,點
,點![]() 在
在![]() 軸上,以
軸上,以![]() 為直徑作
為直徑作![]() ,點
,點![]() 在
在![]() 軸上,且在點
軸上,且在點![]() 上方,過點
上方,過點![]() 作
作![]() 的切線
的切線![]() ,
,![]() 為切點,如果點
為切點,如果點![]() 在第一象限,則稱
在第一象限,則稱![]() 為點
為點![]() 的離點.例如,圖1中的
的離點.例如,圖1中的![]() 為點
為點![]() 的一個離點.
的一個離點.
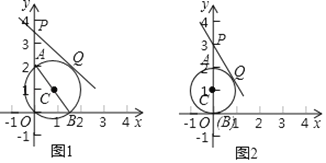
(1)已知點![]() ,
,![]() 為
為![]() 的離點.
的離點.
①如圖2,若![]() ,則圓心
,則圓心![]() 的坐標為__________,線段
的坐標為__________,線段![]() 的長為__________;
的長為__________;
②若![]() ,求線段
,求線段![]() 的長;
的長;
(2)已知![]() ,直線
,直線![]() .
.
①當![]() 時,若直線
時,若直線![]() 上存在
上存在![]() 的離點
的離點![]() ,則點
,則點![]() 縱坐標
縱坐標![]() 的最大值為__________;
的最大值為__________;
②記直線![]() 在
在![]() 的部分為圖形
的部分為圖形![]() ,如果圖形
,如果圖形![]() 上存在
上存在![]() 的離點,直接寫出
的離點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(感知)如圖1,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,將線段
,將線段![]() 繞著點
繞著點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 至線段
至線段![]() ,過點
,過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() ,易知
,易知![]() ,得到點
,得到點![]() 的坐標為
的坐標為![]() .
.
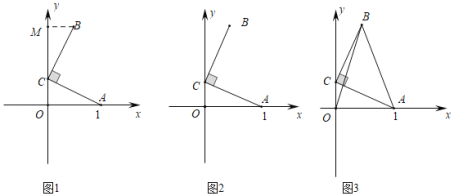
(探究)如圖2,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,將線段
,將線段![]() 繞著點
繞著點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 至線段
至線段![]() .
.
(1)求點![]() 的坐標.(用含
的坐標.(用含![]() 的代數式表示)
的代數式表示)
(2)求出BC所在直線的函數表達式.
(拓展)如圖3,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸上,將線段
軸上,將線段![]() 繞著點
繞著點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 至線段
至線段![]() ,連結
,連結![]() 、
、![]() ,則
,則![]() 的最小值為_______.
的最小值為_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com