
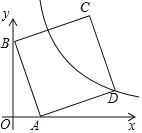
【題目】如圖,在平面直角坐標系中,直線y=﹣4x+4與x軸、y軸分別交于A、B兩點,以AB為邊在第一象限作正方形ABCD,點D在雙曲線y=![]() 上;將正方形ABCD沿x軸負方向平移a個單位長度后,點C恰好落在雙曲線在第一象限的分支上,則a的值是_____.
上;將正方形ABCD沿x軸負方向平移a個單位長度后,點C恰好落在雙曲線在第一象限的分支上,則a的值是_____.
【答案】3
【解析】
根據直線的關系式可以求出A、B的坐標,由正方形可以通過作輔助線,構造全等三角形,進而求出C、D的坐標,求出反比例函數的關系式,進而求出C點 平移后落在反比例函數圖象上的點G的坐標,進而得出平移的距離.
當x=0時,y=4,∴B(0,4),當y=0時,x=1,
∴A(1,0),
∴OA=1,OB=4,
∵ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
過點D、C作DM⊥x軸,CN⊥y軸,垂足為M、N,
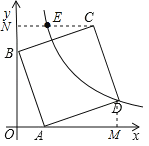
∴∠ABO=∠BCN=∠DAM,
∵∠AOB=∠BNC=∠AMD=90°,
∴△AOB≌△BNC≌△DMA (AAS),
∴OA=DM=BN=1,AM=OB=CN=4
∴OM=1+4=5,ON=4+1=5,
∴C(4,5),D(5,1),
把D(5,1)代入y=![]() 得:k=5,
得:k=5,
∴y=![]() ,
,
當y=5時,x=1,
∴E(1,5),
點C向左平移到E時,平移距離為4﹣1=3,即:a=3,
故答案為:3.


 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案科目:初中數學 來源: 題型:
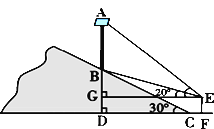
【題目】為了大力弘揚和踐行社會主義核心價值觀,某鄉鎮在一條公路旁的小山坡上,樹立一塊大型標語牌AB,如圖所示,標語牌底部B點到山腳C點的距離BC為20米,山坡的坡角為30°. 某同學在山腳的平地F處測量該標語牌的高,測得點C到測角儀EF的水平距離CF = 1.7米,同時測得標語牌頂部A點的仰角為45°,底部B點的仰角為20°,求標語牌AB的高度.(參考數值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() )
)
【答案】標語牌AB的高度約為12.16米.
【解析】分析:![]() 解直角三角形求處CD的長度,則
解直角三角形求處CD的長度,則![]() 然后在直角
然后在直角![]() 中即可求得
中即可求得![]() 的長,在Rt△AGE中,求得
的長,在Rt△AGE中,求得![]() 的長,從而求得
的長,從而求得![]() 的高度..
的高度..
詳解:在Rt△BDC中,![]() BC = 20米,
BC = 20米,![]()
∴![]()
∴![]()
∴![]()
在Rt△BGE中,![]()
∴![]()
在Rt△AGE中,![]()
∴![]()
∴![]()
答:標語牌AB的高度約為12.16米.
點睛:考查解直角三角形的應用,結合圖形利用三角函數解三角形即可.
【題型】解答題
【結束】
20
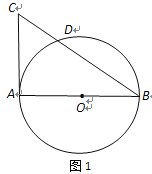
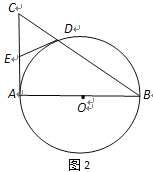
【題目】已知AB是⊙O的直徑,AC是⊙O的切線,BC交⊙O于點D(如圖1).
(1)若AB=2,∠B=30°,求CD的長;
(2) 取AC的中點E,連結D、E(如圖2),求證:DE與⊙O相切.
查看答案和解析>>
科目:初中數學 來源: 題型:
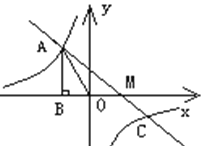
【題目】已知,反比例函數![]() 的圖象過第二象限內的點
的圖象過第二象限內的點![]() ,
,![]() 軸于
軸于![]() ,
,![]() 面積為3,若直線
面積為3,若直線![]() 經過點
經過點![]() ,并且經過反比例函數
,并且經過反比例函數![]() 的圖象上另一點
的圖象上另一點![]() .
.
(1)求反比例函數的解析式;
(2)求直線![]() 解析式
解析式
(3)求![]() 的面積;
的面積;
(4)直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了開發利用海洋資源,某勘測飛機預測量一島嶼兩端A、B的距離,飛機在距海平面垂直高度為100米的點C處測得端點A的俯角為60°,然后沿著平行于AB的方向水平飛行了500米,在點D測得端點B的俯角為45°,求島嶼兩端A、B的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 是關于x的一元二次方程
是關于x的一元二次方程![]() 的兩個實數根.
的兩個實數根.
(1)是否存在實數k,使![]() 成立?若存在,求出k的值;若不存在,請說明理由.
成立?若存在,求出k的值;若不存在,請說明理由.
(2)求使![]() 的值為整數的實數k的整數值.
的值為整數的實數k的整數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
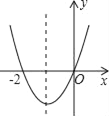
【題目】如圖,根據二次函數y=ax2+bx+c(a≠0)的圖象,有下列幾種說法:
①a+b+c>0;
②該拋物線的對稱軸是直線x=﹣1;
③當x=1時,y=2a;
④am2+bm+a>0(m≠﹣1).
其中正確的個數是( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了增強學生體質,決定開設以下體育課外活動項目:A.籃球 B.乒乓球C.羽毛球 D.足球,為了解學生最喜歡哪一種活動項目,隨機抽取了部分學生進行調查,并將調查結果繪制成了兩幅不完整的統計圖,

請回答下列問題:
(1)這次被調查的學生共有多少人?
(2)請你將條形統計圖(2)補充完整;
(3)在平時的乒乓球項目訓練中,甲、乙、丙、丁四人表現優秀,現決定從這四名同學中任選兩名參加乒乓球比賽,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用100厘米長的鉛絲,彎折成一個長方形的模型.
(1)設長方形的面積為S平方厘米,長方形的長為![]() 厘米,用
厘米,用![]() 的式子表示S;
的式子表示S;
(2)當S=400平方厘米時,求![]() 的值;
的值;
(3)當S=625平方厘米時,求![]() 的值;
的值;
(4)S的值會不會為700平方厘米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C在線段AB上,M、N分別是線段AC、BC的中點,
![]()
(1)若AC=7cm,BC=5cm,求線段MN的長;
(2)若AB=a,點C為線段AB上任意一點,你能用含a的代數式表示MN的長度嗎?若能,請寫出結果與過程,若不能,請說明理由;
(3)若將(2)中“點C為線段AB上任意一點”改為“點C為直線AB上任意一點”,其余條件不變,(2)中的結論是否仍然成立?請畫圖并寫出說明過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com