
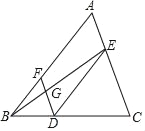
【題目】完成下面的證明:如圖,點D,E,F分別是三角形ABC的邊BC,CA,AB上的點,連接DE,DF,DE∥AB,∠BFD=∠CED,連接BE交DF于點G,求證:∠EGF+∠AEG=180°.
證明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
【答案】兩直線平行,同位角相等;等量代換;同位角相等,兩直線平行;兩直線平行,同旁內角互補.
【解析】
依據兩直線平行, 同位角相等以及等量代換, 即可得到∠A=∠BFD, 再根據同位角相等, 兩直線平行, 即可得出DF//AF, 進而得出∠EGF+∠AEG=180°.
證明:∵DE∥AB(已知),
∴∠A=∠CED(兩直線平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代換)
∴DF∥AE(同位角相等,兩直線平行)
∴∠EGF+∠AEG=180°(兩直線平行,同旁內角互補)
故答案為:兩直線平行,同位角相等;等量代換;同位角相等,兩直線平行;兩直線平行,同旁內角互補.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:
【題目】閱讀理解
如圖1,已知點A是BC外一點,連接AB,AC,求∠BAC+∠B+∠C的度數.
(1)閱讀并補充下面推理過程
解:過點A作ED∥BC
∴∠B=∠ ,∠C=∠ .
又∵∠EAB+∠BAC+∠DAC=180°(平角定義)
∴∠B+∠BAC+∠C=180°
從上面的推理過程中,我們發現平行線具有“等角轉化”的功能,將∠BAC,∠B,∠C“湊”在一起,得出角之間的關系,使問題得以解決
(2)如圖2,已知AB∥ED,求∠B+∠BCD+∠D的度數.
小明受到啟發,過點C作CF∥AB如圖所示,請你幫助小明完成解答:
(3)已知AB∥CD,點C在點D的右側,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直線交于點E,點E在AB與CD兩條平行線之間.
①如圖3,點B在點A的左側,若∠ABC=60°,則∠BED的度數為 °.
②如圖4,點B在點A的右側,且AB<CD,AD<BC.若∠ABC=n°,則∠BED的度數為 °(用含n的代數式表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c(a≠0)與x軸、y軸分別交于點A(3,0)、B(0,3)兩點.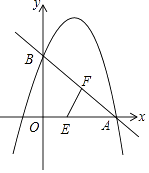
(1)試求拋物線的解析式和直線AB的解析式;
(2)動點E從O點沿OA方向以1個單位/秒的速度向終點A勻速運動,同時動點F沿AB方向以 ![]() 個單位/秒的速度向終點B勻速運動,E、F任意一點到達終點時另一個點停止運動,連接EF,設運動時間為t,當t為何值時△AEF為直角三角形?
個單位/秒的速度向終點B勻速運動,E、F任意一點到達終點時另一個點停止運動,連接EF,設運動時間為t,當t為何值時△AEF為直角三角形?
(3)拋物線位于第一象限的圖象上是否存在一點P,使△PAB面積最大?如果存在,請求出點P的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系xOy中,點A在x軸的正半軸上,點B、C在第一象限,且四邊形OABC是平行四邊形,OC=2 ![]() ,sin∠AOC=
,sin∠AOC= ![]() ,反比例函數y=
,反比例函數y= ![]() 的圖象經過點C以及邊AB的中點D.
的圖象經過點C以及邊AB的中點D. 
(1)求這個反比例函數的解析式;
(2)四邊形OABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點O為坐標原點,我們把橫、縱坐標都為整數的點稱為整點,記定點都是整點的三角形為整點三角形.如圖,已知整點O(0,0),A(2,4),請在所給網格區域(含邊界)上按要求畫圖.
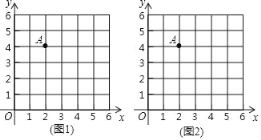
(1)在圖1中畫一個整點三角形OAB,其中點B在第一象限,且點B的橫、縱坐標之和等于點A的橫坐標;
(2)在圖2中畫一個整點三角形OAC,其中點C的坐標為(3t,t),且點C的橫、縱坐標之和是點A的縱坐標的2倍.請直接寫出△OAC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠BAD=60°,AB=2,E是DC邊上一個動點,F是AB邊上一點,∠AEF=30°.設DE=x,圖中某條線段長為y,y與x滿足的函數關系的圖象大致如圖所示,則這條線段可能是圖中的( ).

A. 線段EC B. 線段AE C. 線段EF D. 線段BF
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com