【題目】計算：
（1） 48
(
）- (-48)
(-8) ；
（2） 12 〡0.5〡 
2 (3)2 ]；
（3）先化簡，再求值：
已知m 3， n 
，求3m2n 2mn2 2（mn 
m2n） mn] 3mn2 的值．
科目：初中數(shù)學 來源： 題型：
【題目】一般情況下
不成立，但有些數(shù)可以使得它成立，例如：a＝b＝0．我們稱使得成立的一對數(shù)a，b為“相伴數(shù)對”，記為（a，b）．
(1)若（1，b）是“相伴數(shù)對”，求b的值；
(2)若（m，n）是“相伴數(shù)對”，其中m≠0，求
；
(3)若（m，n）是“相伴數(shù)對”，求代數(shù)式m﹣
﹣[4m﹣2（3n﹣1）]的值．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
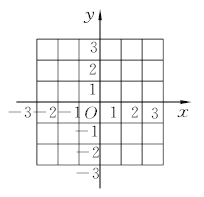
【題目】在平面直角坐標系中,點A關(guān)于y軸的對稱點為點B,點B關(guān)于x軸的對稱點為點C.
(1)若點A的坐標為(1,2),請你在給出的坐標系中畫出ΔABC,設AB與y軸的交點為D,求的值;
(2)若點A的坐標為(a,b)(ab≠0),判斷ΔABC的形狀.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，Rt△ABC中∠C=90°，點O是AB邊上一點，以OA為半徑作⊙O，與邊AC交于點D，連接BD，若∠DBC=∠A，求證：BD是⊙O的切線．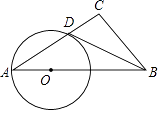 
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在等腰直角三角形MNC中．CN=MN= 
，將△MNC繞點C順時針旋轉(zhuǎn)60°，得到△ABC，連接AM，BM，BM交AC于點O． 
（1）∠NCO的度數(shù)為；
（2）求證：△CAM為等邊三角形；
（3）連接AN，求線段AN的長．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，已知一次函數(shù)y=﹣2x+b的圖象與x軸、y軸分別交于B，A兩點，與反比例函數(shù)y= 
（x＞0）交于C，D兩點．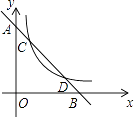
（1）若點D的坐標為（2，m），則m= ， b=；
（2）在（1）的條件下，通過計算判斷AC與BD的數(shù)量關(guān)系；
（3）若在一次函數(shù)y=﹣2x+b與反比例函數(shù)y= （x＞0）的圖象第一象限始終有兩個交點的前提下，不論b為何值，（2）中AC與BD的數(shù)量關(guān)系是否恒成立？試說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】閱讀思考
我們知道，在數(shù)軸上|a|表示數(shù)a所對應的點到原點的距離，這是絕對值的幾何意義，由此我們可進一步地來研究數(shù)軸上任意兩個點之間的距離，一般地，如果數(shù)軸上兩點A、B 對立的數(shù)用a，b表示，那么這兩個點之間的距離AB＝|a﹣b|．也可以用兩點中右邊的點所表示數(shù)的減去左邊的點所表示的數(shù)來計算，例如：數(shù)軸上P，Q兩點表示的數(shù)分別是﹣1和2，那么P，Q兩點之間的距離就是 PQ＝2﹣（﹣1）＝3．
啟發(fā)應用
如圖，點A在數(shù)軸上對應的數(shù)為a，點B對應的數(shù)為b，且a、b滿足|a+3|+（b﹣2）2＝0
（1）求線段AB的長；
（2）如圖，點C在數(shù)軸上對應的數(shù)為x，且x是方程2x+1＝
x﹣8的解，
①求線段BC的長；
②在數(shù)軸上是否存在點P使PA+PB＝BC？若存在，直接寫出點P對應的數(shù)：若不存在，說明理由．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
