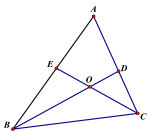
【題目】如圖，已知，△ABC中，∠A=60，BD,CE是△ABC的兩條角平分線，BD,CE相交于點O，求證：BC=CD+BE.
【答案】詳見解析.
【解析】
在BC上找到F使得BF=BE，易證∠BOE=∠COD=60°，即可證明△BOE≌△BOF，可得∠BOF=∠BOE=60°，即可證明△OCF≌△OCD，可得CF=CD，根據BC=BF+CF即可解決問題.
證明：在BC上找到F使得BF=BE，
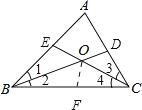
∵∠A=60°，BD、CE是△ABC的角平分線，
∴∠BOC=180°-
（∠ABC+∠ACB）=180°-（180°-∠A）=120°，
∴∠BOE=∠COD=60°，
在△BOE和△BOF中，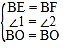
，
∴△BOE≌△BOF，（SAS）
∴∠BOF=∠BOE=60°，
∴∠COF=∠BOC-∠BOF=60°，
在△OCF和△OCD中，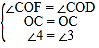
，
∴△OCF≌△OCD（ASA），
∴CF=CD，
∵BC=BF+CF，
∴BC=BE+CD．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
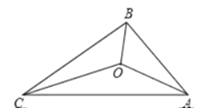
【題目】如圖，△ABC的三邊AB、BC、CA長分別為30、40、50．其三條角平分線交于點O，則S△ABO ：S△BCO ：S△CAO =______ 。
查看答案和解析>>
科目：初中數學 來源： 題型：
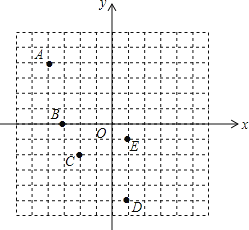
【題目】在平面直角坐標系中，每個小方格的邊長為一個單位長度.
（1）點
的坐標為 .點
的坐標為 .
（2）點
關于
軸對稱點的坐標為 ；
（3）以、
、
為頂點的三角形的面積為 ；
（4）點
在軸上，且
的面積等于
的面積，點的坐標為 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD為矩形，H、F分別為AD、BC邊的中點，四邊形EFGH為矩形，E、G分別在AB、CD邊上，則圖中四個直角三角形面積之和與矩形EFGH的面積之比為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，甲、乙兩人以相同路線前往離學校12千米的地方參加植樹活動．分析甲、乙兩人前往目的地所行駛的路程S（千米）隨時間t（分鐘）變化的函數圖象，解決下列問題：
（1）求出甲、乙兩人所行駛的路程S甲、S乙與t之間的關系式；
（2）甲行駛10分鐘后，甲、乙兩人相距多少千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩艘客輪同時離開港口，航行的速度都是40m/min，甲客輪用15min到達點A，乙客輪用20min到達點B，若A，B兩點的直線距離為1000m，甲客輪沿著北偏東30°的方向航行，則乙客輪的航行方向可能是（ ）
A. 北偏西30° B. 南偏西30° C. 南偏東60° D. 南偏西60°
查看答案和解析>>
科目：初中數學 來源： 題型：
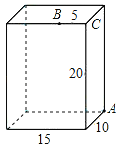
【題目】如圖，一個放置在地面上的長方體，長為15cm，寬為10cm，高為20cm，點B與點C的距離為5cm，一只螞蟻如果要沿著長方體的表面從點A爬到點B，需要爬行的最短距離是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
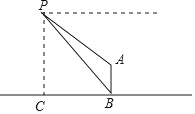
【題目】如圖，一個熱氣球懸停在空中，從熱氣球上的P點測得直立于地面的旗桿AB的頂端A與底端B的俯角分別為34°和45°，此時P點距地面高度PC為75米，求旗桿AB的高度（結果精確到0.1米）．
（參考數據：sin34°=0.56，cos34°=0.83，tan34°=0.67）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在精準扶貧政策的扶持下，貧困戶老李今年試種的百香果獲得大豐收，共收獲2 000千克．扶貧小組幫助他將百香果按照品質從高到低分成A，B，C，D，E五個等級，并根據數據繪制了如下的扇形統計圖和頻數分布表：
請根據圖表信息解答下列問題：
（1）
__________；
__________；
__________；
（2）求扇形統計圖中“E”所對應的圓心角的度數；
（3）為了幫助貧困戶老李銷售百香果，扶貧小組聯系了甲、乙兩位經銷商．他們分別給出如下收購方案：
甲：全部按5元/千克收購；
乙：按等級收購：C等級單價為6.5元/千克，每提高一個等級單價提高1元/千克，剩下的D，E兩個等級單價均為2元/千克．
請你通過計算，判斷哪個經銷商的方案使老李盈利更多．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com