
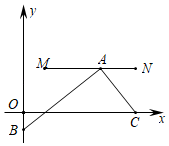
【題目】如圖,在平面直角坐標系中,M、N、C三點的坐標分別為(![]() ,1),(3,1),(3,0),點A為線段MN上的一個動點,連接AC,過點A作AB⊥AC交y軸于點B,當點A從M運動到N時,點B隨之運動,設點B的坐標為(0,b),則b的取值范圍是( )
,1),(3,1),(3,0),點A為線段MN上的一個動點,連接AC,過點A作AB⊥AC交y軸于點B,當點A從M運動到N時,點B隨之運動,設點B的坐標為(0,b),則b的取值范圍是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
【答案】B
【解析】
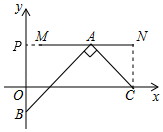
延長NM交y軸于P點,則MN⊥y軸.連接CN.證明△PAB∽△NCA,得出![]() ,設PA=x,則NA=PN﹣PA=3﹣x,設PB=y,代入整理得到y=3x﹣x2=﹣(x﹣
,設PA=x,則NA=PN﹣PA=3﹣x,設PB=y,代入整理得到y=3x﹣x2=﹣(x﹣![]() )2+
)2+![]() ,根據二次函數的性質以及
,根據二次函數的性質以及![]() ≤x≤3,求出y的最大與最小值,進而求出b的取值范圍.
≤x≤3,求出y的最大與最小值,進而求出b的取值范圍.
解:如圖,延長NM交y軸于P點,則MN⊥y軸.連接CN.
在△PAB與△NCA中,
![]() ,
,
∴△PAB∽△NCA,
∴![]() ,
,
設PA=x,則NA=PN﹣PA=3﹣x,設PB=y,
∴![]() ,
,
∴y=3x﹣x2=﹣(x﹣![]() )2+
)2+![]() ,
,
∵﹣1<0,![]() ≤x≤3,
≤x≤3,
∴x=![]() 時,y有最大值
時,y有最大值![]() ,此時b=1﹣
,此時b=1﹣![]() =﹣
=﹣![]() ,
,
x=3時,y有最小值0,此時b=1,
∴b的取值范圍是﹣![]() ≤b≤1.
≤b≤1.
故選:B.


 名題金卷系列答案
名題金卷系列答案 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,一小球沿與地面成一定角度的方向飛出,小球的飛行路線是一條拋物線,如果不考慮空氣阻力,小球的飛行高度y(單位:m)與飛行時間x(單位:s)之間具有函數關系y=﹣5x2+20x,請根據要求解答下列問題:
(1)在飛行過程中,當小球的飛行高度為15m時,飛行時間是多少?
(2)在飛行過程中,小球從飛出到落地所用時間是多少?
(3)在飛行過程中,小球飛行高度何時最大?最大高度是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
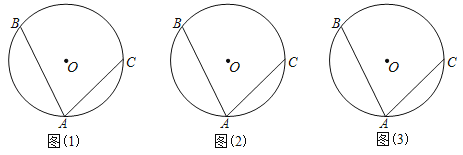
【題目】作圖題:⊙O上有三個點A,B,C,∠BAC=70°,請畫出要求的角,并標注.
(1)畫一個140°的圓心角;(2)畫一個110°的圓周角;(3)畫一個20°的圓周角.
查看答案和解析>>
科目:初中數學 來源: 題型:
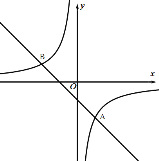
【題目】如圖,一次函數的圖象![]() 與反比例函數的圖象
與反比例函數的圖象![]() 交于A(2,﹣4),B(m, 2)兩點.當x滿足條件______________時,一次函數的值大于反比例函數值.
交于A(2,﹣4),B(m, 2)兩點.當x滿足條件______________時,一次函數的值大于反比例函數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 為倡導“低碳生活”,常選擇以自行車作為代步工具,如圖1所示是一輛自行車的實物圖.車架檔AC與CD的長分別為45cm,60cm,且它們互相垂直,座桿CE的長為20cm,點A,C,E在同一條直線上,且∠CAB=75°,如圖2.
(1)求車架檔AD的長;
(2)求車座點E到車架檔AB的距離.
(結果精確到1 cm.參考數據: sin75°="0.966," cos75°=0.259,tan75°=3.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:我們知道,四邊形的一條對角線把這個四邊形分成了兩個三角形,如果這兩個三角形相似(不全等),我們就把這條對角線叫做這個四邊形的“相似對角線”.
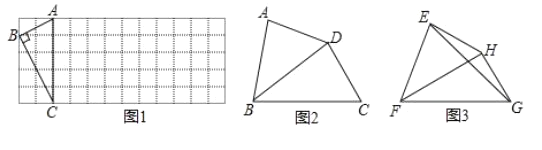
理解:
(1)如圖1,已知Rt△ABC在正方形網格中,請你只用無刻度的直尺在網格中找到一點 D,使四邊形ABCD是以AC為“相似對角線”的四邊形(畫出1個即可);
(2)如圖2,在四邊形ABCD中,![]() ,對角線BD平分∠ABC.
,對角線BD平分∠ABC.
求證: BD是四邊形ABCD的“相似對角線”;
運用:
(3)如圖3,已知FH是四邊形EFGH的“相似對角線”,∠EFH=∠HFG=![]() .連接EG,若△EFG的面積為
.連接EG,若△EFG的面積為![]() ,求FH的長.
,求FH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請閱讀以下材料,并完成相應的任務:

任務:
(1)設P(a,![]() ),R(b,
),R(b,![]() ),求直線OM的函數解析式(用含a,b的代數式表示),并說明Q點在直線OM上;
),求直線OM的函數解析式(用含a,b的代數式表示),并說明Q點在直線OM上;
(2)證明:∠MOB=![]() ∠AOB.
∠AOB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一”小長假期間,某超市為了吸引顧客,設計了一種促銷活動:在一個不透明的箱子里放有4個相同的小球,球上分別標有“0元”、“10元”、“20元”、“30元”的字樣.規定:顧客在本超市一次性購物滿500元以上均可獲得兩次摸球的機會(摸出小球后放回).超市根據兩小球所標金額的和返還相應的代金券.
(1)顧客甲購物1000元,則他最少可獲 元代金券,最多可獲 元代金券.
(2)請用樹形圖或列表方法,求出顧客甲獲得不低于30元(含30元)代金券的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com