
【題目】如圖1,是由一些大小相同的小正方體組合成的簡單幾何體,并放在墻角.(注:圖3、圖4、圖5每一個小方格的邊長為1cm)
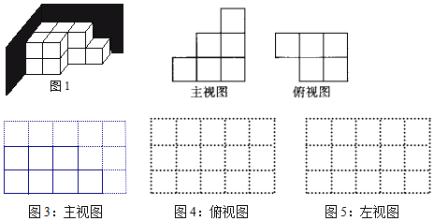
(1)該幾何體主視圖如圖3所示,請在圖4方格紙中畫出它的俯視圖;
(2)若將其露在外面的表面涂一層漆,則其涂漆面積為 cm2.(正方體的棱長為1cm)
(3)用一些小立方塊搭一個幾何體,使它的主視圖和俯視圖如圖所示,它最少需要多少個小立方塊?最多需要多少個小立方塊?并在圖5方格紙中畫出需要最多小立方塊的幾何體的左視圖.
【答案】(1)見解析;(2)16;(3)最少需要8個小立方塊,最多需要11個小立方塊,圖見解析
【解析】
(1)由已知條件可知,俯視圖有4列,每列小正方數形數目分別為2,2,1,1.據此可畫出圖形;
(2)先求出露在外面的面數,再乘以1個面的面積即可求解;
(3)依據“俯視打地基,主視瘋狂蓋”可得到它最少需要多少個小立方塊,最多需要多少個小立方塊,并在圖5方格紙中畫出需要最多小立方塊的幾何體的左視圖即可求解.
解:(1)如圖所示:
(2)1×1×(7+5+4)
=1×16
=16(cm2).
故其涂漆面積為16cm2.
故答案為:16.
(3)如圖所示:
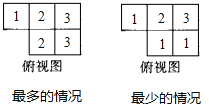
由圖知,最少需要8個小立方塊,最多需要11個小立方塊,
需要最多小立方塊的幾何體的左視圖如下:



 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:初中數學 來源: 題型:
【題目】實驗探究:
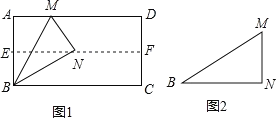
(1)如圖1,對折矩形紙片ABCD,使AD與BC重合,得到折痕EF,把紙片展開;再一次折疊紙片,使點A落在EF上,并使折痕經過點B,得到折痕BM,同時得到線段BN,MN.請你觀察圖1,猜想∠MBN的度數是多少,并證明你的結論.
(2)將圖1中的三角形紙片BMN剪下,如圖2,折疊該紙片,探究MN與BM的數量關系,寫出折疊方案,并結合方案證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解題:
拆項法是因式分解中一種技巧較強的方法,它通常是把多項式中的某一項拆成幾項,再分組分解,因而有時需要多次實驗才能成功,例如把![]() 分解因式,這是一個三項式,最高次項是三次項,一次項系數為零,本題既沒有公因式可提取,又不能直接應用公式,因而考慮制造分組分解的條件,把常數項拆成1和3,原式就變成
分解因式,這是一個三項式,最高次項是三次項,一次項系數為零,本題既沒有公因式可提取,又不能直接應用公式,因而考慮制造分組分解的條件,把常數項拆成1和3,原式就變成![]() ,再利用立方和與平方差先分解,解法如下:
,再利用立方和與平方差先分解,解法如下:
原式![]()
![]()
公式:![]() ,
,![]()
根據上述論法和解法,
(1)因式分解:![]() ;
;
(2)因式分解:![]() ;
;
(3)因式分解:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(-4,2)、B(0,4)、C(0,2),
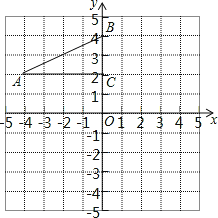
(1)畫出△ABC關于點C成中心對稱的△A1B1C;平移△ABC,若點A的對應點A2的坐標為(0,-4),畫出平移后對應的△A2B2C2;
(2)△A1B1C和△A2B2C2關于某一點成中心對稱,則對稱中心的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
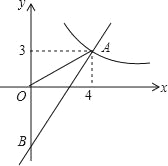
【題目】如圖,一次函數y=kx+b的圖象分別與反比例函數y=![]() 的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
(1)求函數y=kx+b和y=![]() 的表達式;
的表達式;
(2)已知點C(0,5),試在該一次函數圖象上確定一點M,使得MB=MC,求此時點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,點D,E分別是邊BC,AB上的中點,連接DE并延長至點F,使EF=2DF,連接CE、AF.
(1)證明:AF=CE;
(2)當∠B=30°時,試判斷四邊形ACEF的形狀并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格中,每個小正方形的邊長為1個單位長度.△ABC的三個頂點都在格點上.
⑴ 在線段AC上找一點P(不能借助圓規),使得![]() ,畫出點P的位置,并說明理由.
,畫出點P的位置,并說明理由.
⑵ 求出⑴中線段PA的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了豐富課外活動,某校將購買一些乒乓球拍和乒乓球,某商場銷售一種乒乓球拍和乒乓球,乒乓球拍每副定價80元,乒乓球每盒定價20元,“國慶節”期間商場決定開展促銷活動,活動期間向客戶提供兩種優惠方案.
方案一:買一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定價的90%付款.
某校要到該商場購買乒乓球拍20副,乒乓球![]() 盒(
盒(![]() >20且為整數).
>20且為整數).
(1)若按方案一購買,需付款 元(用含![]() 的整式表示,要化簡); 若按方案二購買,需付款 元(用含
的整式表示,要化簡); 若按方案二購買,需付款 元(用含![]() 的整式表示,要化簡).
的整式表示,要化簡).
(2)若![]() 30,通過計算說明此時按哪種方案購買較為合算?
30,通過計算說明此時按哪種方案購買較為合算?
(3)當![]() 30時,你能給出一種更為省錢的購買方案嗎?試寫出你的購買方法.
30時,你能給出一種更為省錢的購買方案嗎?試寫出你的購買方法.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com