
【題目】觀察探究,解決問題.在四邊形ABCD中,點E、F、G、H分別是邊AB、BC、CD、DA的中點,順次連接E、F、G、H得到的四邊形EFGH叫做中點四邊形.
(1)如圖1,求證:中點四邊形EFGH是平行四邊形;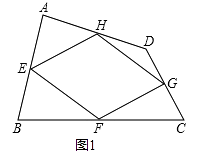
(2)請你探究并填空:
①當四邊形ABCD變成平行四邊形時,它的中點四邊形是;
②當四邊形ABCD變成矩形時,它的中點四邊形是;
③當四邊形ABCD變成正方形時,它的中點四邊形是;
(3)如圖2,當中點四邊形EFGH為矩形時,對角線EG與FH相交于點O,P為EH上的動點,過點P作PM⊥EG,PN⊥FH,垂足分別為M、N,若EF=a,FG=b,請判斷PM+PN的長是否為定值?若是,求出此定值;若不是,說明理由.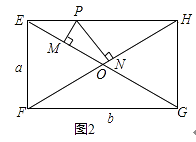
【答案】
(1)
解:連接AC,如圖1,
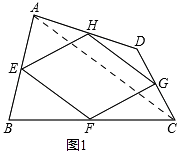
在△DAC中,HG∥AC,且HG= ![]() AC,
AC,
在△BAC中,EF∥AC,且EF= ![]() AC,
AC,
∴HG∥EF,且HG=EF,
∴四邊形EFGH是平行四邊形
(2)平行四邊形;菱形;正方形
(3)
解:如圖,
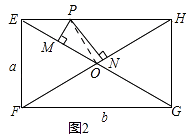
連接PO,
在矩形EFGH中:EO=HO= ![]() EG=
EG= ![]()
![]() ,
,
∵S△EOH= ![]() S四邊形EFGH=
S四邊形EFGH= ![]() ab=S△POE+S△POH,
ab=S△POE+S△POH,
∴ ![]() PM×EO+
PM×EO+ ![]() PN×HO=
PN×HO= ![]() ab,
ab,
∴ ![]()
![]() (PM+PN)=
(PM+PN)= ![]() ab,
ab,
∴PM+PN= ![]() .
.
故PM+PN是定值
【解析】解: (2)①在△DAC中,HG∥AC,且HG= ![]() AC,
AC,
在△BAC中,EF∥AC,且EF= ![]() AC,
AC,
∴HG∥EF,且HG=EF,
∴四邊形EFGH是平行四邊形.
所以答案是平行四邊形,
②由(1)有,四邊形EFGH是平行四邊形.
同(1)的方法得,EH= ![]() BD,
BD,
∵四邊形ABCD是矩形,
∴AC=BD
∴EH=EF,
∴平行四邊形ABCD是菱形;
所以答案是菱形,
③由(2)②有,四邊形EFGH是菱形.
∵四邊形ABCD是正方形,
∴AC⊥BD,
∴∠EFG=90°,
∴菱形ABCD是正方形;
所以答案是正方形,


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】在給定的條件中,能畫出平行四邊形的是( )
A. 以60cm為一條對角線,20cm,34cm為兩條鄰邊
B. 以6cm,10cm為兩條對角線,8cm為一邊
C. 以20cm,36cm為兩條對角線,22cm為一邊
D. 以6cm為一條對角線,3cm,10cm為兩條鄰邊
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于鈍角α,定義它的三角函數值如下:
sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α)
(1)求sin120°,cos120°,sin150°的值;
(2)若一個三角形的三個內角的比是1:1:4,A,B是這個三角形的兩個頂點,sinA,cosB是方程4x2﹣mx﹣1=0的兩個不相等的實數根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=32°,以A為圓心,任意長為半徑畫弧分別交AB , AC于點M和N , 再分別以M , N為圓心,大于 ![]() MN的長為半徑畫弧,兩弧交于點P , 連接AP并延長交BC于點D , 則下列說法:
MN的長為半徑畫弧,兩弧交于點P , 連接AP并延長交BC于點D , 則下列說法: 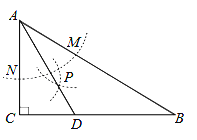
①AD是∠BAC的平分線;
②CD是△ADC的高;
③點D在AB的垂直平分線上;
④∠ADC=61°.
其中正確的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數y=(1-m)x的圖象上有兩點A(x1,y1),B(x2,y2),且當x1>x2時,y1>y2,則m的取值范圍是( )
A. m<0 B. m>0 C. m<1 D. m>1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題:
某小區為改善居住環境,計劃在小區內種植甲、乙兩種花木共6600棵,若甲種花木的數量是乙種花木數量的2倍少300棵.甲、乙兩種花木的數量分別是多少棵?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com