
【題目】如圖,線段AB=4,C為線段AB上的一個動點,以AC、BC為邊作等邊△ACD和等邊△BCE,⊙O外接于△CDE,則⊙O半徑的最小值為( )

A. 4 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】B
【解析】
分別作∠A與∠B角平分線,交點為P.由三線合一可知AP與BP為CD、CE垂直平分線;再由垂徑定理可知圓心O在CD、CE垂直平分線上,則交點P與圓心O重合,即圓心O是一個定點;連OC,若半徑OC最短,則OC⊥AB,由△AOB為底邊4,底角30°的等腰三角形,可求得OC=![]() .
.
如圖,分別作∠A與∠B角平分線,交點為P,
∵△ACD和△BCE都是等邊三角形,
∴AP與BP為CD、CE垂直平分線,
又∵圓心O在CD、CE垂直平分線上,則交點P與圓心O重合,即圓心O是一個定點;
連接OC,
若半徑OC最短,則OC⊥AB,
又∵∠OAC=∠OBC=30°,AB=4,
∴OA=OB,
∴AC=BC=2,
∴在直角△AOC中,OC=ACtan∠OAC=2×tan30°=![]() ,
,
故選B.


科目:初中數學 來源: 題型:
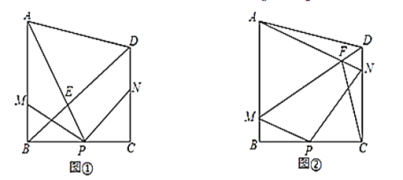
【題目】如圖,在四邊形![]() 中,
中,![]() 點
點![]() 從點
從點![]() 出發以
出發以![]() 的速度沿
的速度沿![]() 向點
向點![]() 勻速移動,點
勻速移動,點![]() 從點
從點![]() 出發以
出發以![]() 的速度沿
的速度沿![]() 向點
向點![]() 勻速移動,點
勻速移動,點![]() 從點
從點![]() 出發以
出發以![]() 的速度沿
的速度沿![]() 向點
向點![]() 勻速移動.點
勻速移動.點![]() 同時出發,當其中一個點到達終點時,其他兩個點也隨之停止運動,設移動時間為
同時出發,當其中一個點到達終點時,其他兩個點也隨之停止運動,設移動時間為![]() .
.
(1)如圖①,
①當![]() 為何值時,點
為何值時,點![]() 為頂點的三角形與
為頂點的三角形與![]() 全等?并求出相應的
全等?并求出相應的![]() 的值;
的值;
②連接![]() 交于點
交于點![]() ,當
,當![]() 時,求出
時,求出![]() 的值;
的值;
(2)如圖②,連接![]() 交于點
交于點![]() .當
.當![]() 時,證明:
時,證明:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小林在某商店購買商品A、B共三次,只有一次購買時,商品A、B同時打折(折扣相同),其余兩次均按標價購買.三次購買商品A、B的數量和費用如下表:
購買商品A的數量/個 | 購買商品B的數量/個 | 購買總費用/元 | |
第一次購物 | 6 | 5 | 1140 |
第二次購物 | 3 | 7 | 1110 |
第三次購物 | 9 | 8 | 1062 |
(1)小林以折扣價購買商品A、B是第 次購物;
(2)求出商品A、B的標價;
(3)若商品A、B的折扣相同,問商店是打幾折出售這兩種商品的?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩輛摩托車同時從相距20km的A,B兩地出發,相向而行.圖中l 1,l 2分別表示甲、乙兩輛摩托車到A地的距離s(km)與行駛時間t(h)的函數關系.則下列說法錯誤的是( )

A.乙摩托車的速度較快B.經過0.3小時甲摩托車行駛到A,B兩地的中點
C.當乙摩托車到達A地時,甲摩托車距離A地![]() kmD.經過
kmD.經過![]() 小時兩摩托車相遇
小時兩摩托車相遇
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD中,AB//DC,AB=DC,且AB=6cm,BC=8cm,對角線AC =10cm,
(1)求證:四邊形ABCD是矩形;
(2)如圖(2),若動點Q從點C出發,在CA邊上以每秒5cm的速度向點A勻速運動,同時動點P從點B出發,在BC邊上以每秒4cm的速度向點C勻速運動,運動時間為t秒(0≤t<2),連接BQ、AP,若AP⊥BQ,求t的值;
(3)如圖(3),若點Q在對角線AC上,CQ=4cm,動點P從B點出發,以每秒1cm的速度沿BC運動至點C止.設點P運動了t秒,請你探索:從運動開始,經過多少時間,以點Q、P、C為頂點的三角形是等腰三角形?請求出所有可能的結果.

查看答案和解析>>
科目:初中數學 來源: 題型:
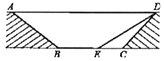
【題目】為緩解交通擁堵,遵義市某區擬計劃修建一地下通道,該通道一部分的截面如圖所示(圖中地面AD與通道BC平行),通道水平寬度BC為8米,∠BCD=135°,通道斜面CD 的長為6米,通道斜面AB的坡度i=1:![]()
(1)求通道斜面AB的長為多少米;
(2)為增加市民行走的舒適度,擬將設計圖中的通道斜面CD的坡度變緩,修改后的通道斜面DE的坡角為30°,求此時BE的長.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半徑為2的⊙C, 分別交AC、BC于點D、E,得到
.半徑為2的⊙C, 分別交AC、BC于點D、E,得到![]() .
.
(1)求證:AB為⊙C的切線;
(2)求圖中陰影部分的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=k1x+b(k1≠0)的圖象分別與x軸,y軸相交于點A,B,與反比例函數y2=![]() 的圖象相交于點C(﹣4,﹣2),D(2,4).
的圖象相交于點C(﹣4,﹣2),D(2,4).
(1)求一次函數和反比例函數的表達式;
(2)當x為何值時,y1>0;
(3)當x為何值時,y1<y2,請直接寫出x的取值范圍.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com