
【題目】在平面直角坐標系![]() 中,對于點
中,對于點![]() 和點
和點![]() 給出如下定義:若
給出如下定義:若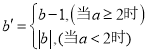 ,則稱點
,則稱點![]() 為點
為點![]() 的限變點.例如:點
的限變點.例如:點![]() 的限變點的坐標是
的限變點的坐標是![]() 點
點![]() 的限變點的坐標是
的限變點的坐標是![]() 點
點![]() 的限變點的坐標是
的限變點的坐標是![]() .
.
![]() ①點
①點![]() 的限變點的坐標是 ;
的限變點的坐標是 ;
②在點![]() 中有一個點是雙曲線
中有一個點是雙曲線![]() 上某一個點的限變點,這個點是(填“
上某一個點的限變點,這個點是(填“![]() ”或“
”或“![]() ”)
”)
![]() 若點
若點![]() 在關于
在關于![]() 的二次函數
的二次函數![]() 的圖象上,其限變點
的圖象上,其限變點![]() 的縱坐標
的縱坐標![]() 的取值范圍是
的取值范圍是![]() 或
或![]() 其中
其中![]() .令
.令![]() ,直接寫出
,直接寫出![]() 的值.
的值.
![]() 若點
若點![]() 在函數
在函數![]() 的圖象上,其限變點
的圖象上,其限變點![]() 的縱坐標
的縱坐標![]() 的取值范圍是
的取值范圍是![]() ,直接寫出
,直接寫出![]() 的取值范圍;
的取值范圍;
【答案】![]() ①
①![]() ;②
;②![]() ;
; ![]() ;
; ![]() 的取值范圍時:
的取值范圍時:![]()
【解析】
(1)①a=![]() <2,故b=
<2,故b=![]() =1,故答案為
=1,故答案為![]() ;
;
②假設限變點A(-2,2)對應的原點為:(-2,2)或(-2,-2),這兩個點都不在反比例函數圖像上;假設限變點B(1,3)對應的原點應該為:(1,2),點(1,2)在反比例函數圖像上,即可求解;
(2)依題意,![]() 圖像上的點P的限變點Q必在函數
圖像上的點P的限變點Q必在函數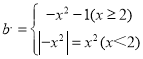 的圖像上,當x=2時,y=-4-1=-5,即點B(2,-5),b=-5,故當x≥2時,b=y≤-5,當x<2時,y= b≥0,m=0,n=-5,s=m-n=5;
的圖像上,當x=2時,y=-4-1=-5,即點B(2,-5),b=-5,故當x≥2時,b=y≤-5,當x<2時,y= b≥0,m=0,n=-5,s=m-n=5;
(3)依題意,y=x-3(-2≤x≤k,k>-2)圖像上的點P的限變點Q必在函數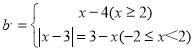 的圖像上,當x=2時,b取最小值,b=2-4=-2,當b=5時,x-4=5或-x+3=5,∴x=9或x=-2,當b=1時,x-4=1,x=5,即可求解.
的圖像上,當x=2時,b取最小值,b=2-4=-2,當b=5時,x-4=5或-x+3=5,∴x=9或x=-2,當b=1時,x-4=1,x=5,即可求解.
解:(1)① a=![]() <2,故b=
<2,故b=![]() =1,故答案為
=1,故答案為![]() ;
;
②假設限變點A(-2,2)對應的原點為:(-2,2)或(-2,-2),這兩個點都不在反比例函數圖像上;
假設限變點B(1,3)對應的原點應該為:(1,2),點(1,2)在反比例函數圖像上;
故答案為B.
(2)依題意,![]() 圖像上的點P的限變點Q必在函數
圖像上的點P的限變點Q必在函數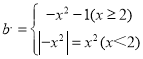 的圖像上(如圖1),
的圖像上(如圖1),
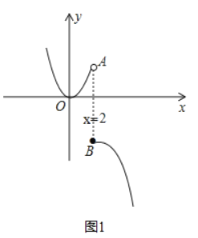
當x=2時,y=-4-1=-5,即點B(2,-5),b=-5,故當x≥2時,b=y≤-5,當x<2時,y= b≥0,m=0,n=-5,s=m-n=5;
(3)依題意,y=x-3(-2≤x≤k,k>-2)圖像上的點P的限變點Q必在函數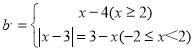

當x=2時,b取最小值,b=2-4=-2,
當b=5時,x-4=5或-x+3=5,∴x=9或x=-2,
當b=1時,x-4=1,x=5,
∵-2≤b≤5
∴由圖像知,k的取值范圍是![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,圖象過點(﹣1,0),對稱軸為直線x=1,下列結論:①2a+b=0;②9a+c>3b;③若點A(﹣3,y1)、點B(﹣![]() ,y2)、點C(
,y2)、點C(![]() ,y3)在該函數圖象上,則y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的兩根為x1和x2,且x1<x2,則x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正確的結論有( )
,y3)在該函數圖象上,則y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的兩根為x1和x2,且x1<x2,則x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正確的結論有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
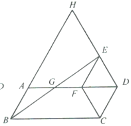
【題目】如圖,以平行四邊形ABCD的較短邊CD為一邊作菱形CDEF,使點F落在邊AD上,連接BE,交AF于點G,延長DE,BA交于點H,若∠ADC=60°,則![]() =________
=________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀與應用:同學們,你們已經知道![]() ,即
,即![]() .所以
.所以![]() (當且僅當
(當且僅當![]() 時取等號).
時取等號).
閱讀1:若![]() 為實數,且
為實數,且![]() (當且僅當
(當且僅當![]() 時取等號).
時取等號).
閱讀2:若函數![]() (
(![]() ,
,![]() ,
,![]() 為常數).由閱讀1結論可知:
為常數).由閱讀1結論可知:![]() 即
即![]() ,∴當
,∴當![]() 即
即![]() 時,函數
時,函數![]() 的最小值為
的最小值為![]() .
.
閱讀理解上述內容,解答下列問題:
問題1:若函數![]() ,則
,則![]() = 時,函數
= 時,函數![]() 的最小值為 .
的最小值為 .
問題2:已知一個矩形的面積為4,其中一邊長為![]() ,則另一邊長為
,則另一邊長為![]() ,周長為
,周長為![]() ,求當
,求當![]() 時,矩形周長的最小值為 .
時,矩形周長的最小值為 .
問題3:求代數式![]() 的最小值.
的最小值.
問題4:建造一個容積為8立方米,深2米的長方體無蓋水池,池底和池壁的造價分別為每平方米![]() 米,水池總造價為
米,水池總造價為![]() (元),求當
(元),求當![]() 為多少時,水池總造價
為多少時,水池總造價![]() 最低?最低是多少?
最低?最低是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定,以二次函數y=ax2+bx+c的二次項系數a的2倍為一次項系數,一次項系數b為常數項構造的一次函數y=2ax+b叫做二次函數y=ax2+bx+c的“子函數”,反過來,二次函數y=ax2+bx+c叫做一次函數y=2ax+b的“母函數”.
(1)若一次函數y=2x-4是二次函數y=ax2+bx+c的“子函數”,且二次函數經過點(3,0),求此二次函數的解析式及頂點坐標.
(2)若“子函數”y=x-6的“母函數”的最小值為1,求“母函數”的函數表達式.
(3)已知二次函數y=-x2-4x+8的“子函數”圖象直線l與x軸、y軸交于C、D兩點,動點P為二次函數y=-x2-4x+8對稱軸右側上的動點,求△PCD的面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在ABCD中,已知AB=6,BE平分∠ABC交AD邊于點E,點E將AD分為1:3兩部分,則AD的長為( )
A. 8或24B. 8C. 24D. 9或24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 為原點,拋物線
為原點,拋物線![]() 經過點
經過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為點
的對稱點為點![]() .過點
.過點![]() 作直線
作直線![]() 軸,交
軸,交![]() 軸于點
軸于點![]() .
.
(Ⅰ)求該拋物線的解析式及對稱軸;
(Ⅱ)點![]() 在
在![]() 軸上,當
軸上,當![]() 的值最小時,求點
的值最小時,求點![]() 的坐標;
的坐標;
(Ⅲ)拋物線上是否存在點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com