
【題目】拋物線y=ax2+bx+3(a≠0)經過點A(﹣1,0),B(![]() ,0),且與y軸相交于點C.
,0),且與y軸相交于點C.
(1)求這條拋物線的表達式;
(2)求∠ACB的度數;
(3)點D是拋物線上的一動點,是否存在點D,使得tan∠DCB=tan∠ACO.若存在,請求出點D的坐標,若不存在,說明理由.

【答案】(1)y=﹣2x2+x+3;(2)∠ACB=45°;(3)D點坐標為(1,2)或(4,﹣25).
【解析】
(1)設交點式y=a(x+1)(x﹣![]() ),展開得到﹣
),展開得到﹣![]() a=3,然后求出a即可得到拋物線解析式;
a=3,然后求出a即可得到拋物線解析式;
(2)作AE⊥BC于E,如圖1,先確定C(0,3),再分別計算出AC=![]() ,BC=
,BC=![]() ,接著利用面積法計算出AE=
,接著利用面積法計算出AE=![]() ,然后根據三角函數的定義求出∠ACE即可;
,然后根據三角函數的定義求出∠ACE即可;
(3)作BH⊥CD于H,如圖2,設H(m,n),證明Rt△BCH∽Rt△ACO,利用相似計算出BH=![]() ,CH=
,CH=![]() ,再根據兩點間的距離公式得到(m﹣
,再根據兩點間的距離公式得到(m﹣![]() )2+n2=(
)2+n2=(![]() )2,m2+(n﹣3)2=(
)2,m2+(n﹣3)2=(![]() )2,接著通過解方程組得到H(
)2,接著通過解方程組得到H(![]() ,﹣
,﹣![]() )或(
)或(![]() ),然后求出直線CD的解析式,與二次函數聯立成方程組,解方程組即可.
),然后求出直線CD的解析式,與二次函數聯立成方程組,解方程組即可.
(1)設拋物線解析式為y=a(x+1)(x﹣![]() ),即y=ax2﹣
),即y=ax2﹣![]() ax﹣
ax﹣![]() a,∴﹣
a,∴﹣![]() a=3,解得:a=﹣2,∴拋物線解析式為y=﹣2x2+x+3;
a=3,解得:a=﹣2,∴拋物線解析式為y=﹣2x2+x+3;
(2)作AE⊥BC于E,如圖1,當x=0時,y=﹣2x2+x+3=3,則C(0,3),而A(﹣1,0),B(![]() ,0),∴AC=
,0),∴AC=![]() =
=![]() ,BC=
,BC=![]() =
=![]()
![]() AEBC=
AEBC=![]() OCAB,∴AE=
OCAB,∴AE=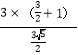 =
=![]() .
.
在Rt△ACE中,sin∠ACE=![]() =
=![]() =
=![]() ,∴∠ACE=45°,即∠ACB=45°;
,∴∠ACE=45°,即∠ACB=45°;
(3)作BH⊥CD于H,如圖2,設H(m,n).
∵tan∠DCB=tan∠ACO,∴∠HCB=∠ACO,∴Rt△BCH∽Rt△ACO,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,∴BH=
,∴BH=![]() ,CH=
,CH=![]() ,∴(m﹣
,∴(m﹣![]() )2+n2=(
)2+n2=(![]() )2=
)2=![]() ,①
,①
m2+(n﹣3)2=(![]() )2=
)2=![]() ,②
,②
②﹣①得m=2n+![]() ,③,把③代入①得:(2n+
,③,把③代入①得:(2n+![]() ﹣
﹣![]() )2+n2=
)2+n2=![]() ,整理得:80n2﹣48n﹣9=0,解得:n1=﹣
,整理得:80n2﹣48n﹣9=0,解得:n1=﹣![]() ,n2=
,n2=![]() .
.
當n=﹣![]() 時,m=2n+
時,m=2n+![]() =
=![]() ,此時H(
,此時H(![]() ,﹣
,﹣![]() ),易得直線CD的解析式為y=﹣7x+3,解方程組
),易得直線CD的解析式為y=﹣7x+3,解方程組![]() 得:
得:![]() 或
或![]() ,此時D點坐標為(4,﹣25);
,此時D點坐標為(4,﹣25);
當n=![]() 時,m=2n+
時,m=2n+![]() =
=![]() ,此時H(
,此時H(![]() ),易得直線CD的解析式為y=﹣x+3,解方程組
),易得直線CD的解析式為y=﹣x+3,解方程組![]() 得:
得:![]() 或
或![]() ,此時D點坐標為(1,2).
,此時D點坐標為(1,2).
綜上所述:D點坐標為(1,2)或(4,﹣25).


科目:初中數學 來源: 題型:
【題目】已知△ABC中,D為AB邊上任意一點,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α,
(1)如圖1所示,當α=60°時,求證:△DCE是等邊三角形;
(2)如圖2所示,當α=45°時,求證:![]() =
=![]() ;
;
(3)如圖3所示,當α為任意銳角時,請直接寫出線段CE與DE的數量關系:![]() =_____.
=_____.



查看答案和解析>>
科目:初中數學 來源: 題型:
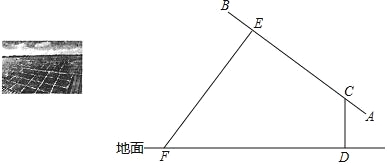
【題目】太陽能光伏發電因其清潔、安全、便利、高效等特點,已成為世界各國普遍關注和重點發展的新興產業.如圖是太陽能電池板支撐架的截面圖,其中線段AB、CD、EF表示支撐角鋼,太陽能電池板緊貼在支撐角鋼AB上且長度均為300cm,AB的傾斜角為30°,BE=CA=50cm,支撐角鋼CD、EF與地面接觸點分別為D、F,CD垂直于地面,FE⊥AB于點E.點A到地面的垂直距離為50cm,求支撐角鋼CD和EF的長度各是多少.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
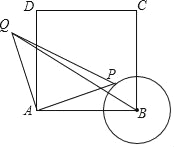
【題目】如圖,正方形ABCD中,AB=3,以B為圓心,![]() AB長為半徑畫圓B,點P在圓B上移動,連接AP,并將AP繞點A逆時針旋轉90°至Q,連接BQ,在點P移動過程中,BQ長度的最小值為_____.
AB長為半徑畫圓B,點P在圓B上移動,連接AP,并將AP繞點A逆時針旋轉90°至Q,連接BQ,在點P移動過程中,BQ長度的最小值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是邊AB上一點,以BD為直徑的⊙O經過點E,且交BC于點F.
(1)求證:AC是⊙O的切線;
(2)若BF=6,⊙O的半徑為5,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,∠B=90°,AB=8,CB=6,P、Q是△ABC邊上的兩個動點,其中點P從點A開始沿A→B方向運動,且速度為每秒1cm,點Q從點B開始沿B→C方向運動,且速度為每秒2cm,它們同時出發,設出發的時間為t秒.

(1)當t=2秒時,求PQ的長;
(2)求出發時間為幾秒時,△PQB是等腰三角形?
(3)若Q沿B→C→A方向運動,則當點Q在邊CA上運動時,求能使△BCQ成為等腰三角形的運動時間。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名同學的家與學校的距離均為![]() .甲同學先步行
.甲同學先步行![]() ,然后乘公交車去學校;乙同學騎自行車去學校.已知乙同學騎自行車的速度是甲同學步行速度的一倍,公交車的速度是乙同學騎自行車速度的
,然后乘公交車去學校;乙同學騎自行車去學校.已知乙同學騎自行車的速度是甲同學步行速度的一倍,公交車的速度是乙同學騎自行車速度的![]() 倍.甲、乙兩名同學同時從家出發去學校,結果甲同學比乙同學早到
倍.甲、乙兩名同學同時從家出發去學校,結果甲同學比乙同學早到![]() .
.
(1)解:設乙同學騎自行車的速度為![]() .完成表格:
.完成表格:
乙同學 | 甲同學 | ||
騎自行車 | 步行 | 乘公交車 | |
路程 |
|
| |
時間 |
| ||
(2)求乙同學騎自行車的速度.
(3)當甲同學到達學校時,乙同學離學校還有多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】由于霧霾天氣頻發,市場上防護口罩出現熱銷,某醫藥公司每月固定生產甲、乙兩種型號的防霧霾口罩共20萬只,且所有產品當月全部售出,原料成本、銷售單價及工人生產提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
銷售單價 | 18 | 12 |
生產提成 | 1 | 0.8 |
(1)若該公司五月份的銷售收入為300萬元,求甲、乙兩種型號的產品分別是多少萬只?
(2)公司實行計件工資制,即工人每生產一只口罩獲得一定金額的提成,如果公司六月份投入總成本(原料總成本+生產提成總額)不超過239萬元,應怎樣安排甲、乙兩種型號的產量,可使該月公司所獲利潤最大?并求出最大利潤(利潤=銷售收入﹣投入總成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年春北方嚴重干旱,某社區人畜飲水緊張,每天需從社區外調運飲用水120噸,有關部門緊急部署,從甲、乙兩水廠調運飲用水到社區供水點,甲廠每天最多可調出80噸,乙廠每天最多可調出90噸,從兩水廠運水到社區供水點的路程和運費如下表:
到社區供水點的路程(千米) | 運費(元/噸·千米) | |
甲廠 | 20 | 12 |
乙廠 | 14 | 15 |
【1】若某天調運水的總運費為26700元,則從甲、乙兩水廠各調運多少噸飲用水?
【2】設從甲廠調運飲用水![]() 噸,總運費為W元,試寫出W關于與
噸,總運費為W元,試寫出W關于與![]() 的函數關系式,怎樣安排調運方案才能使每天的總運費最省?
的函數關系式,怎樣安排調運方案才能使每天的總運費最省?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com