
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,直線
兩點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .點
.點![]() 是拋物線上一動點,過點
是拋物線上一動點,過點![]() 作直線
作直線![]() 軸于點
軸于點![]() ,交直線
,交直線![]() 于點
于點![]() .設(shè)點
.設(shè)點![]() 的橫坐標為
的橫坐標為![]() .
.
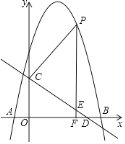
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 若點
若點![]() 在
在![]() 軸上方的拋物線上,當
軸上方的拋物線上,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
![]() 若點
若點![]() ’是點
’是點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點,當點
的對稱點,當點![]() ’落在
’落在![]() 軸上時,請直接寫出
軸上時,請直接寫出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 的坐標為
的坐標為![]() 或
或![]() ;(3)m的值為
;(3)m的值為![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系數(shù)法求出拋物線的解析式;
(2)用含m的代數(shù)式分別表示出PE、EF,然后列方程求解;
(3)解題關(guān)鍵是識別出當四邊形PECE′是菱形,然后根據(jù)PE=CE的條件,列出方程求解;當四邊形PECE′是菱形不存在時,P點y軸上,即可得到m的值.
解:![]() ∵拋物線
∵拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,
兩點,
∴![]() ,
,
解得![]() ,
,
∴拋物線的解析式為![]() .
.
![]() ∵點
∵點![]() 的橫坐標為
的橫坐標為![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
![]() .
.
由題意,![]() ,即:
,即:![]()
①若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() .
.
由題意,![]() 的取值范圍為:
的取值范圍為:![]() ,故
,故![]() 、
、![]() 這兩個解均舍去.
這兩個解均舍去.
∴![]() 或
或![]() .
.
∴點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
![]() 假設(shè)存在.
假設(shè)存在.
作出示意圖如下:
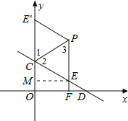
∵點![]() 、
、![]() 關(guān)于直線
關(guān)于直線![]() 對稱,
對稱,
∴![]() ,
,![]() ,
,![]() .
.
∵![]() 平行于
平行于![]() 軸,∴
軸,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,即四邊形
,即四邊形![]() 是菱形.
是菱形.
當四邊形![]() 是菱形存在時,
是菱形存在時,
由直線![]() 解析式
解析式![]() ,可得
,可得![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() .
.
過點![]() 作
作![]() 軸,交
軸,交![]() 軸于點
軸于點![]() ,易得
,易得![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() ,又由
,又由![]() 可知:
可知:![]()
∴![]() .
.
①若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,解得
,解得![]() ,
,![]() .
.
由題意,![]() 的取值范圍為:
的取值范圍為:![]() ,故
,故![]() 這個解舍去.
這個解舍去.
當四邊形![]() 是菱形這一條件不存在時,
是菱形這一條件不存在時,
此時![]() 點橫坐標為
點橫坐標為![]() ,
,![]() ,
,![]() ,
,![]() 三點重合與
三點重合與![]() 軸上,也符合題意,
軸上,也符合題意,
∴![]() ,
,
綜上所述,存在滿足條件的![]() 的值為
的值為![]() 或
或![]() 或
或![]() 或
或![]() .
.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC中,∠BAC=80°,若MP和NQ分別垂直平分AB和AC.
(1)求∠PAQ的度數(shù).
(2)若△APQ周長為12,BC長為8,求PQ的長.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,D是△ABC外接圓上的動點,且B,D位于AC的兩側(cè),DE⊥AB,垂足為E,DE的延長線交此圓于點F.BG⊥AD,垂足為G,BG交DE于點H,DC,F(xiàn)B的延長線交于點P,且PC=PB.
(1)求證:BG∥CD;
(2)設(shè)△ABC外接圓的圓心為O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
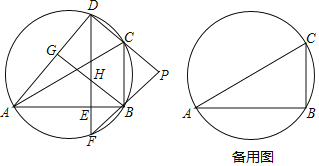
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知拋物線的頂點為A(1,4),拋物線與y軸交于點B(0,3),與x軸交于C、D兩點.點P是x軸上的一個動點.
(1)求此拋物線的解析式;
(2)求C、D兩點坐標及△BCD的面積;
(3)若點P在x軸上方的拋物線上,滿足S△PCD=![]() S△BCD,求點P的坐標.
S△BCD,求點P的坐標.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,點D是BC的中點,點E、F分別是線段AD及其延長線上,且DE=DF,給出下列條件:①BE⊥EC;②BF∥EC;③AB=AC,從中選擇一個條件使四邊形BECF是菱形,并給出證明,你選擇的條件是___(只填寫序號).

證明:
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC、△CDE均為等邊三角形,連接BD、AE交于點O,BC與AE交于于點P.

(1)求證:△ACE ≌ △BCD.
(2)求∠AOB的度數(shù).
(3)連接OC,求證:OC平分∠AOD
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線與x軸相交于點A(﹣2,0)、B(4,0),與y軸交于點C(0,﹣4),BC與拋物線的對稱軸相交于點D.
(1)求該拋物線的表達式,并直接寫出點D的坐標;
(2)過點A作AE⊥AC交拋物線于點E,求點E的坐標.
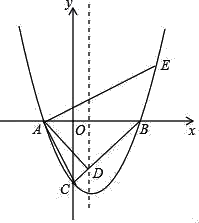
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直角坐標系![]() 中,一次函數(shù)
中,一次函數(shù)![]() 的圖像
的圖像![]() 分別與
分別與![]() ,
,![]() 軸交于
軸交于![]() ,
,![]() 兩點,正比例函數(shù)的圖像
兩點,正比例函數(shù)的圖像![]() 與
與![]() 交于點
交于點![]()
![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函數(shù)![]() 的圖像為
的圖像為![]() ,且
,且![]() ,
,![]() ,
,![]() 不能圍成三角形,直接寫出
不能圍成三角形,直接寫出![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com