
【題目】如圖,拋物線y=ax2+bx+3經(jīng)過點(diǎn) B(﹣1,0),C(2,3),拋物線與y軸的焦點(diǎn)A,與x軸的另一個焦點(diǎn)為D,點(diǎn)M為線段AD上的一動點(diǎn),設(shè)點(diǎn)M的橫坐標(biāo)為t.
(1)求拋物線的表達(dá)式;
(2)過點(diǎn)M作y軸的平行線,交拋物線于點(diǎn)P,設(shè)線段PM的長為1,當(dāng)t為何值時,1的長最大,并求最大值;(先根據(jù)題目畫圖,再計算)
(3)在(2)的條件下,當(dāng)t為何值時,△PAD的面積最大?并求最大值;
(4)在(2)的條件下,是否存在點(diǎn)P,使△PAD為直角三角形?若存在,直接寫出t的值;若不存在,說明理由.

【答案】(1)y=﹣x2+2x+3;(2)當(dāng)t=![]() 時,l有最大值,l最大=
時,l有最大值,l最大=![]() ;(3)t=
;(3)t=![]() 時,△PAD的面積的最大值為
時,△PAD的面積的最大值為![]() ;(4)t=
;(4)t=![]() .
.
【解析】試題分析:(1)利用待定系數(shù)法即可解決問題;
(2)易知直線AD解析式為y=-x+3,設(shè)M點(diǎn)橫坐標(biāo)為m,則P(t,-t2+2t+3),M(t,-t+3),可得l=-t2+2t+3-(-t+3)=-t2+3t=-(t-![]() )2+
)2+![]() ,利用二次函數(shù)的性質(zhì)即可解決問題;
,利用二次函數(shù)的性質(zhì)即可解決問題;
(3)由S△PAD=![]() ×PM×(xD-xA)=
×PM×(xD-xA)=![]() PM,推出PM的值最大時,△PAD的面積最大;
PM,推出PM的值最大時,△PAD的面積最大;
(4)如圖設(shè)AD的中點(diǎn)為K,設(shè)P(t,-t2+2t+3).由△PAD是直角三角形,推出PK=![]() AD,可得(t-
AD,可得(t-![]() )2+(-t2+2t+3-
)2+(-t2+2t+3-![]() )2=
)2=![]() ×18,解方程即可解決問題;
×18,解方程即可解決問題;
試題解析:(1)把點(diǎn) B(﹣1,0),C(2,3)代入y=ax2+bx+3,
則有![]() ,
,
解得![]() ,
,
∴拋物線的解析式為y=﹣x2+2x+3.
(2)在y=﹣x2+2x+3中,令y=0可得0=﹣x2+2x+3,解得x=﹣1或x=3,
∴D(3,0),且A(0,3),
∴直線AD解析式為y=﹣x+3,
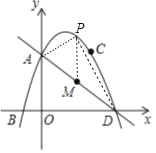
設(shè)M點(diǎn)橫坐標(biāo)為m,則P(t,﹣t2+2t+3),M(t,﹣t+3),
∵0<t<3,
∴點(diǎn)M在第一象限內(nèi),
∴l=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t=﹣(t﹣![]() )2+
)2+![]() ,
,
∴當(dāng)t=![]() 時,l有最大值,l最大=
時,l有最大值,l最大=![]() ;
;
(3)∵S△PAD=![]() ×PM×(xD﹣xA)=
×PM×(xD﹣xA)=![]() PM,
PM,
∴PM的值最大時,△PAD的面積中點(diǎn),最大值=![]() ×
×![]() =
=![]() .
.
∴t=![]() 時,△PAD的面積的最大值為
時,△PAD的面積的最大值為![]() .
.
(4)如圖設(shè)AD的中點(diǎn)為K,設(shè)P(t,﹣t2+2t+3).

∵△PAD是直角三角形,
∴PK=![]() AD,
AD,
∴(t﹣![]() )2+(﹣t2+2t+3﹣
)2+(﹣t2+2t+3﹣![]() )2=
)2=![]() ×18,
×18,
整理得t(t﹣3)(t2﹣t﹣1)=0,
解得t=0或3或![]() ,
,
∵點(diǎn)P在第一象限,
∴t=![]() .
.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學(xué)業(yè)考試導(dǎo)與練系列答案
初中學(xué)業(yè)考試導(dǎo)與練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O的直徑,延長AB到點(diǎn)C,使得2BC=3OB,D是⊙O上一點(diǎn),連接AD,CD,過點(diǎn)A作CD的垂線,交CD的延長線于點(diǎn)F,過點(diǎn)D作DE⊥AC于點(diǎn)E,且DE=DF.
(1)求證:CD是⊙O的切線;
(2)若AB=4.
①求DF的長;
②連接OF,交AD于點(diǎn)M,求DM的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
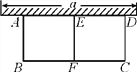
【題目】如圖,有長為24 m的籬笆,一面利用墻(墻的最大可用長度a為10 m)圍成中間隔著一道籬笆的長方形花圃.
(1)現(xiàn)要圍成面積為45 m2的花圃,則AB的長是多少米?
(2)現(xiàn)要圍成面積為48 m2的花圃能行嗎?若能行,則AB的長是多少?若不能行,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形AOBC是正方形,OA=4,動點(diǎn)P從點(diǎn)O出發(fā),沿折線OACB方向以1個單位/秒的速度勻速運(yùn)動,另一個點(diǎn)Q從O出發(fā),沿折線OBCA方向以2個單位/秒的速度勻速運(yùn)動,運(yùn)動時間為t秒,當(dāng)它們相遇時停止運(yùn)動,當(dāng)以A、P、B、Q四點(diǎn)為頂點(diǎn)的四邊形為平行四邊形時,t的值為______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將函數(shù)y=![]() (x﹣2)2+1的圖象沿y軸向上平移得到一條新函數(shù)的圖象,其中點(diǎn)A(1,m),B(4,n)平移后的對應(yīng)點(diǎn)分別為點(diǎn)A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數(shù)表達(dá)式是( )
(x﹣2)2+1的圖象沿y軸向上平移得到一條新函數(shù)的圖象,其中點(diǎn)A(1,m),B(4,n)平移后的對應(yīng)點(diǎn)分別為點(diǎn)A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數(shù)表達(dá)式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】唐山質(zhì)量監(jiān)督局從某食品廠生產(chǎn)的袋裝食品中抽出樣品20袋,檢測每袋的質(zhì)量是否符合標(biāo)準(zhǔn),把超過或不足的部分分別用正、負(fù)數(shù)來表示,記錄如下表:
與標(biāo)準(zhǔn)質(zhì)量的差值(單位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋數(shù) | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的標(biāo)準(zhǔn)質(zhì)量為450克,則抽樣檢測的20袋食品的總質(zhì)量是多少克?
(2)若該種食品的合格標(biāo)準(zhǔn)為450±5克,求該種食品抽樣檢測的合格率?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
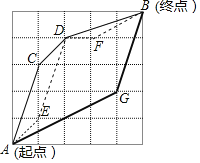
【題目】嘉嘉參加機(jī)器人設(shè)計活動,需操控機(jī)器人在5×5的棋盤格上從A點(diǎn)行走至B點(diǎn),且每個小方格皆為正方形,主辦單位規(guī)定了三條行走路徑R1,R2,R2,其行經(jīng)位置如圖與表所示:
路徑 | 編號 | 圖例 | 行徑位置 |
第一條路徑 | R1 | … | A→C→D→B |
第二條路徑 | R2 | … | A→E→D→F→B |
第三條路徑 | R3 | … | A→G→B |
已知A,B,C,D,E,F,G七點(diǎn)皆落在格線的交點(diǎn)上,且兩點(diǎn)之間的路徑皆為線段.
(1)分別計算出三條路徑的長;
(2)最長的路徑是______ (寫出編號),最短的路徑是 _______(寫出編號).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)的圖象交坐標(biāo)軸于A(﹣1,0),B(4,0),C(0,﹣4)三點(diǎn),點(diǎn)P是直線BC下方拋物線上一動點(diǎn).
(1)求這個二次函數(shù)的解析式;
(2)是否存在點(diǎn)P,使△POC是以O(shè)C為底邊的等腰三角形?若存在,求出P點(diǎn)坐標(biāo);若不存在,請說明理由;
(3)動點(diǎn)P運(yùn)動到什么位置時,△PBC面積最大,求出此時P點(diǎn)坐標(biāo)和△PBC的最大面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場用24000元購入一批空調(diào),然后以每臺3000元的價格銷售,因天氣炎熱,空調(diào)很快售完;商場又以52000元的價格再次購入該種型號的空調(diào),數(shù)量是第一次購入的2倍,但購入的單價上調(diào)了200元,售價每臺也上調(diào)了200元.
(1)商場第一次購入的空調(diào)每臺進(jìn)價是多少元?
(2)商場既要盡快售完第二次購入的空調(diào),又要在這兩次空調(diào)銷售中獲得的利潤率不低于22%,打算將第二次購入的部分空調(diào)按每臺九五折出售,最多可將多少臺空調(diào)打折出售?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com