
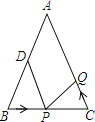
【題目】如圖![]() ,
,![]() 厘米,
厘米,![]() ,
,![]() 厘米,點
厘米,點![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上以4厘米/秒的速度由
上以4厘米/秒的速度由![]() 點向
點向![]() 點運動,同時,點
點運動,同時,點![]() 在線段
在線段![]() 上由
上由![]() 點向
點向![]() 點運動,若點
點運動,若點![]() 的運動速度為
的運動速度為![]() 厘米/秒,則當
厘米/秒,則當![]() 與
與![]() 全等時,
全等時,![]() 的值為_____厘米/秒.
的值為_____厘米/秒.

【答案】4或6
【解析】
此題要分兩種情況:①當BD=PC時,△BPD與△CQP全等,計算出BP的長,進而可得運動時間,然后再求v;②當BD=CQ時,△BDP≌△QCP,計算出BP的長,進而可得運動時間,然后再求v.
解:當BD=PC時,△BPD與△CQP全等,
∵點D為AB的中點,
∴BD=![]() AB=12cm,
AB=12cm,
∵BD=PC,
∴BP=16-12=4(cm),
∵點P在線段BC上以4厘米/秒的速度由B點向C點運動,
∴運動時間時1s,
∵△DBP≌△PCQ,
∴BP=CQ=4cm,
∴v=4÷1=4厘米/秒;
當BD=CQ時,△BDP≌△QCP,
∵BD=12cm,PB=PC,
∴QC=12cm,
∵BC=16cm,
∴BP=4cm,
∴運動時間為4÷2=2(s),
∴v=12÷2=6厘米/秒.
故答案為:4或6.


科目:初中數(shù)學 來源: 題型:
【題目】八年級(1)班學生在完成課題學習“體質(zhì)健康測試中的數(shù)據(jù)分析”后,利用課外活動時間積極參加體育鍛煉,每位同學從籃球、跳繩、立定跳遠、長跑、鉛球中選一項進行訓練,訓練后都進行了測試.現(xiàn)將項目選擇情況及訓練后籃球定時定點投籃測試成績整理后作出如下統(tǒng)計圖.

請你根據(jù)上面提供的信息回答下列問題:
(1)扇形圖中跳繩部分的扇形圓心角為 度,該班共有學生 人, 訓練后籃球定時定點投籃平均每個人的進球數(shù)是 .
(2)老師決定從選擇鉛球訓練的3名男生和1名女生中任選兩名學生先進行測試,請用列表或畫樹形圖的方法求恰好選中兩名男生的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某商家到梧州市一茶廠購買茶葉,購買茶葉數(shù)量為x千克(x>0),總費用為y元,現(xiàn)有兩種購買方式.
方式一:若商家贊助廠家建設費11500元,則所購茶葉價格為130元/千克;(總費用=贊助廠家建設費+購買茶葉費)
方式二:總費用y(元)與購買茶葉數(shù)量x(千克)滿足下列關系式:y=![]() .
.
請回答下面問題:
(1)寫出購買方式一的y與x的函數(shù)關系式;
(2)如果購買茶葉超過150千克,說明選擇哪種方式購買更省錢;
(3)甲商家采用方式一購買,乙商家采用方式二購買,兩商家共購買茶葉400千克,總費用共計74600元,求乙商家購買茶葉多少千克?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分線DE交AB于D,交BC于E,若CE=3cm,則BE的長為( )

A.6cm B.5cm C.4cm D.3cm
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于點M,連接CM.
(1)求證:BE=AD;并用含α的式子表示∠AMB的度數(shù);
(2)當α=90°時,取AD,BE的中點分別為點P、Q,連接CP,CQ,PQ,如圖2,判斷△CPQ的形狀,并加以證明.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】寧波城區(qū)中考體育選測項目進行了現(xiàn)場抽取,最終確定了寧波城區(qū)2018年體育選測項目:跳繩、籃球運動投籃、立定跳遠,某中學隨機抽取了一部分九年級女同學進行1分鐘跳繩抽測,將測得的成績繪制成如下的統(tǒng)計圖表:

級別 | 成績 | 頻數(shù) |
A |
| 2 |
B |
| 7 |
C |
| 14 |
D |
| 12 |
E |
|
![]() 本次隨機抽取了______名九年級女同學;
本次隨機抽取了______名九年級女同學;
![]() 頻數(shù)分布表中,成績是E級的頻數(shù)是多少?
頻數(shù)分布表中,成績是E級的頻數(shù)是多少?
![]() 若認定“D,E”兩個級別的成績?yōu)?/span>“優(yōu)秀”,全校九年級女同學共有200人,請估計該校跳繩成績優(yōu)秀的女同學人數(shù).
若認定“D,E”兩個級別的成績?yōu)?/span>“優(yōu)秀”,全校九年級女同學共有200人,請估計該校跳繩成績優(yōu)秀的女同學人數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】若二次函數(shù)![]() 和
和![]() 的圖象關于原點成中心對稱,我們就稱其中一個函數(shù)是另一個函數(shù)的中心對稱函數(shù),也稱函數(shù)
的圖象關于原點成中心對稱,我們就稱其中一個函數(shù)是另一個函數(shù)的中心對稱函數(shù),也稱函數(shù)![]() 和
和![]() 互為中心對稱函數(shù).
互為中心對稱函數(shù).
![]() 求函數(shù)
求函數(shù)![]() 的中心對稱函數(shù);
的中心對稱函數(shù);
![]() 如圖,在平面直角坐標系xOy中,E,F(xiàn)兩點的坐標分別為
如圖,在平面直角坐標系xOy中,E,F(xiàn)兩點的坐標分別為![]() ,
,![]() ,二次函數(shù)
,二次函數(shù)![]() 的圖象經(jīng)過點E和原點O,頂點為
的圖象經(jīng)過點E和原點O,頂點為![]() 已知函數(shù)
已知函數(shù)![]() 和
和![]() 互為中心對稱函數(shù);
互為中心對稱函數(shù);
![]() 請在圖中作出二次函數(shù)
請在圖中作出二次函數(shù)![]() 的頂點
的頂點![]() 作圖工具不限
作圖工具不限![]() ,并畫出函數(shù)
,并畫出函數(shù)![]() 的大致圖象;
的大致圖象;
![]() 當四邊形EPFQ是矩形時,請求出a的值;
當四邊形EPFQ是矩形時,請求出a的值;
![]() 已知二次函數(shù)
已知二次函數(shù)![]() 和
和![]() 互為中心對稱函數(shù),且
互為中心對稱函數(shù),且![]() 的圖象經(jīng)過
的圖象經(jīng)過![]() 的頂點當
的頂點當![]() 時,求代數(shù)式
時,求代數(shù)式![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】勾股定理是幾何中的一個重要定理.在我國古算書《周髀算經(jīng)》中就有“若勾三,股四,則弦五”的記載.如圖1是由邊長相等的小正方形和直角三角形構(gòu)成的,可以用其面積關系驗證勾股定理.圖2是把圖1放入長方形內(nèi)得到的,![]() ,AB=3,AC=4,點D,E,F,G,H,I都在長方形KLMJ的邊上,則長方形KLMJ的面積為___.
,AB=3,AC=4,點D,E,F,G,H,I都在長方形KLMJ的邊上,則長方形KLMJ的面積為___.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直角坐標系中,點 A( 2,2)、B(0,1)點 P 在 x 軸上,且△PAB 的等腰三角形,則滿足條件的點 P 共有()個

A.1B.2C.3D.4
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com