
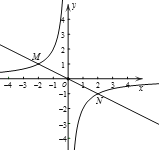
【題目】如圖,反比例函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象分別交于M,N兩點,已知點M(-2,m).
的圖象分別交于M,N兩點,已知點M(-2,m).
(1)求反比例函數的表達式;
(2)點P為y軸上的一點,當∠MPN為直角時,直接寫出點P的坐標.
【答案】(1)![]() ;(2)(0,
;(2)(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
試題(1)把M(﹣2,m)代入函數式y=﹣![]() x中,求得m的值,從而求得M的坐標,代入y=
x中,求得m的值,從而求得M的坐標,代入y=![]() 可求出函數解析式;(2)根據M的坐標求得N的坐標,設P(0,m),根據勾股定理列出關于m的方程,解方程即可求得m進而求得P的坐標.
可求出函數解析式;(2)根據M的坐標求得N的坐標,設P(0,m),根據勾股定理列出關于m的方程,解方程即可求得m進而求得P的坐標.
試題解析:(1)∵點M(﹣2,m)在正比例函數y=﹣![]() x的圖象上,
x的圖象上,
∴m=﹣![]() ×(﹣2)=1,
×(﹣2)=1,
∴M(﹣2,1),
∵反比例函數y=![]() 的圖象經過點M(﹣2,1),
的圖象經過點M(﹣2,1),
∴k=﹣2×1=﹣2.
∴反比例函數的解析式為
(2)∵正比例函數y=﹣![]() x的圖象與反比例函數y=
x的圖象與反比例函數y=![]() 的圖象分別交于M,N兩點,點M(﹣2,1),
的圖象分別交于M,N兩點,點M(﹣2,1),
∴N(2,﹣1),
∵點P為y軸上的一點,
∴設P(0,m),
∵∠MPN為直角,
∴△MPN是直角三角形,
∴(0+2)2+(m﹣1)2+(0﹣2)2+(m+1)2=(2+2)2+(﹣1﹣1)2,
解得m=±![]()
∴點P的坐標為(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠A=110°,E,F分別是邊AB和BC的中點,EP⊥CD于點P,則∠FPC=( )
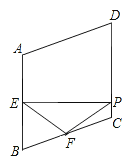
A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店以每件20元的價格購進一批商品,如果以每件30元銷售,那么半月內可售出400件.根據銷售經驗,銷售單價每提高1元,半月內的銷售量相應減少20件.如何提高銷售單價,才能在半月內獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
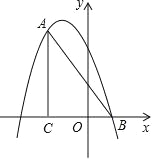
【題目】如圖,在平面直角坐標系中,∠ACB=90°,OC=2BO,AC=6,點B的坐標為(1,0),拋物線y=﹣x2+bx+c經過A、B兩點.
(1)求點A的坐標;
(2)求拋物線的解析式;
(3)點P是直線AB上方拋物線上的一點,過點P作PD垂直x軸于點D,交線段AB于點E,使PE=![]() DE.
DE.
①求點P的坐標;
②在直線PD上是否存在點M,使△ABM為直角三角形?若存在,求出符合條件的所有點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小磊要制作一個三角形的鋼架模型,在這個三角形中,長度為x(單位:cm)的邊與這條邊上的高之和為40 cm,這個三角形的面積S(單位:cm2)隨x(單位:cm)的變化而變化.
(1)請直接寫出S與x之間的函數關系式(不要求寫出自變量x的取值范圍);
(2)當x是多少時,這個三角形面積S最大?最大面積是多少?![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知點A(1,2),B(3,2),連接AB. 若對于平面內一點P,線段AB上都存在點Q,使得PQ≤1,則稱點P是線段AB的“臨近點”.
中,已知點A(1,2),B(3,2),連接AB. 若對于平面內一點P,線段AB上都存在點Q,使得PQ≤1,則稱點P是線段AB的“臨近點”.
(1)在點C(0,2),D(2,![]() ),E(4,1)中,線段AB的“臨近點”是__________;
),E(4,1)中,線段AB的“臨近點”是__________;
(2)若點M(m,n)在直線![]() 上,且是線段AB的“臨近點”,求m的取值范圍;
上,且是線段AB的“臨近點”,求m的取值范圍;
(3)若直線![]() 上存在線段AB的“臨近點”,求b的取值范圍.
上存在線段AB的“臨近點”,求b的取值范圍.
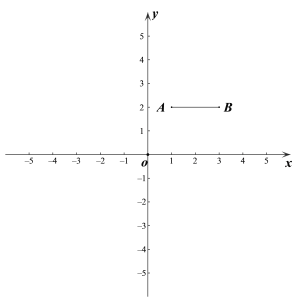
查看答案和解析>>
科目:初中數學 來源: 題型:
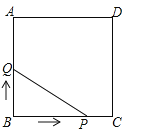
【題目】(3分)如圖,正方形ABCD的邊長為3cm,動點P從B點出發以3cm/s的速度沿著邊BC﹣CD﹣DA運動,到達A點停止運動;另一動點Q同時從B點出發,以1cm/s的速度沿著邊BA向A點運動,到達A點停止運動.設P點運動時間為x(s),△BPQ的面積為y(cm2),則y關于x的函數圖象是( )
A.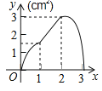 B.
B.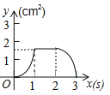 C.
C.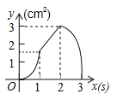 D.
D.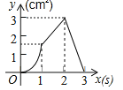
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知點A(1,2),B(3,2),連接AB. 若對于平面內一點P,線段AB上都存在點Q,使得PQ≤1,則稱點P是線段AB的“臨近點”.
中,已知點A(1,2),B(3,2),連接AB. 若對于平面內一點P,線段AB上都存在點Q,使得PQ≤1,則稱點P是線段AB的“臨近點”.
(1)在點C(0,2),D(2,![]() ),E(4,1)中,線段AB的“臨近點”是__________;
),E(4,1)中,線段AB的“臨近點”是__________;
(2)若點M(m,n)在直線![]() 上,且是線段AB的“臨近點”,求m的取值范圍;
上,且是線段AB的“臨近點”,求m的取值范圍;
(3)若直線![]() 上存在線段AB的“臨近點”,求b的取值范圍.
上存在線段AB的“臨近點”,求b的取值范圍.
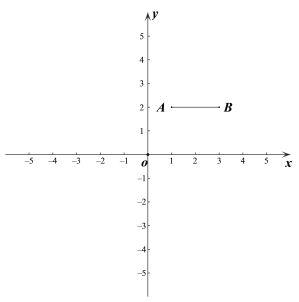
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com