
【題目】某校舉辦學生綜合素質(zhì)大賽,分“單人項目”和“雙人項目”兩種形式,比賽題目包括下列五類:![]() .人文藝術(shù);
.人文藝術(shù);![]() .歷史社會;
.歷史社會;![]() .自然科學;
.自然科學;![]() .天文地理;
.天文地理;![]() .體育健康.
.體育健康.
(1)若小明參加“單人項目”,他從中抽取一個題目,那么恰好抽中“自然科學”類題目的概率為_____.
(2)小林和小麗參加“雙人項目”,比賽規(guī)定:同一小組的兩名同學的題目類型不能相同,且每人只能抽取一次,求他們抽到“天文地理”和“體育健康”類題目的概率是多少?(用畫樹狀圖或列表的方法求解).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)小明一共有五種不同的選擇,所以恰好抽中“自然科學”類題目的概率為![]() .
.
(2)由同一小組的兩名同學的題目類型不能相同,且每人只能抽取一次可知第一名同學抽取之后,第二名同學只能有四種選擇,所以畫樹狀圖可知一共有20種情況,
而他們抽到“天文地理”和“體育健康”類題目有兩次機會,所以概率是![]() .
.
解:(1)∵比賽題目共包括五類:A.人文藝術(shù);B.歷史社會;C.自然科學;D.天文地理;E.體育健康
∴小明恰好抽中“自然科學”類題目的概率為![]()
故答案為:![]() .
.
(2)由題意畫樹狀圖為: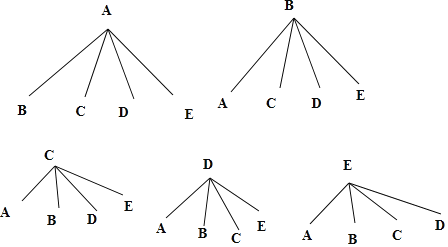
有圖可知他們抽到“天文地理”和“體育健康”類題目的概率是:![]()
∴他們抽到“天文地理”和“體育健康”類題目的概率是:![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】同學們參加綜合實踐活動時,看到木工師傅用“三弧法”在板材邊角處作直角,其作法是:如圖:
(1)作線段AB,分別以點A,B為圓心,AB長為半徑作弧,兩弧交于點C;
(2)以點C為圓心,仍以AB長為半徑作弧交AC的延長線于點D;
(3)連接BD,BC.
根據(jù)以上作圖過程及所作圖形,下列結(jié)論中錯誤的是( )

A.∠ABD=90°B.CA=CB=CDC.sinA=![]() D.cosD=
D.cosD=![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,以![]() 的一邊
的一邊![]() 為直徑的
為直徑的![]() 交
交![]() 于點
于點![]() ,點
,點![]() 是弧
是弧![]() 的中點,連接
的中點,連接![]() 并延長交
并延長交![]() 于點
于點![]() .
.
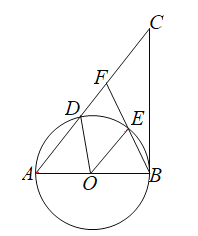
(1)求證:![]() ;
;
(2)①若![]() ,當弧
,當弧![]() 的長度是______時,四邊形
的長度是______時,四邊形![]() 是菱形;
是菱形;
②在①的情況下,當![]() ______時,
______時,![]() 是
是![]() 的切線.
的切線.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=4,AD=8,點E為AD上一點,將△ABE沿BE折疊得到△FBE,點G為CD上一點,將△DEG沿EG折疊得到△HEG,且E、F、H三點共線,當△CGH為直角三角形時,AE的長為________.
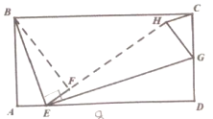
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖①,在矩形![]() 中,
中,![]() ,對角線
,對角線![]() 相交于點
相交于點![]() ,動點
,動點![]() 由點
由點![]() 出發(fā),沿
出發(fā),沿![]() 向點
向點![]() 運動.設(shè)點
運動.設(shè)點![]() 的運動路程為
的運動路程為![]() ,
,![]() 的面積為
的面積為![]() ,
,![]() 與
與![]() 的函數(shù)關(guān)系圖象如圖②所示,則
的函數(shù)關(guān)系圖象如圖②所示,則![]() 邊的長為( ).
邊的長為( ).
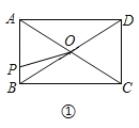
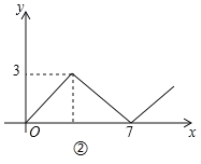
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖象交
的圖象交![]() 軸于點
軸于點![]() ,點
,點![]() ,交
,交![]() 軸于點
軸于點![]()

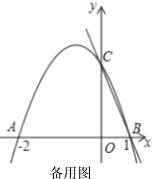
(1)求二次函數(shù)的解析式;
(2)連接![]() ,在直線
,在直線![]() 上方的拋物線上有一點
上方的拋物線上有一點![]() ,過點
,過點![]() 作
作![]() 軸的平行線,交直線
軸的平行線,交直線![]() 于點
于點![]() ,設(shè)點
,設(shè)點![]() 的橫坐標為
的橫坐標為![]() ,線段
,線段![]() 的長為
的長為![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)若點![]() 在
在![]() 軸上,是否存在點
軸上,是否存在點![]() ,使以
,使以![]() 、
、![]() 、
、![]() 為頂點的三角形是等腰三角形,若存在,直接寫出點
為頂點的三角形是等腰三角形,若存在,直接寫出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】設(shè)![]() 是邊長為
是邊長為![]() 的正三角形內(nèi)的一點,
的正三角形內(nèi)的一點,![]() 到三邊的距離分別為
到三邊的距離分別為![]() .若以
.若以![]() 為邊可以組成三角形,則
為邊可以組成三角形,則![]() 應(yīng)滿足的條件為()
應(yīng)滿足的條件為()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】隨著新冠肺炎的爆發(fā),市場對口罩的需求量急劇增大.某口罩生產(chǎn)商自二月份以來,--直積極恢復產(chǎn)能,每日口罩生產(chǎn)量![]() (百萬個)與天數(shù)
(百萬個)與天數(shù)![]() 且
且![]() 為整數(shù))的函數(shù)關(guān)系圖象如圖所示,而該生產(chǎn)商對口供應(yīng)市場對口罩的需求量<(百萬個)與天數(shù)
為整數(shù))的函數(shù)關(guān)系圖象如圖所示,而該生產(chǎn)商對口供應(yīng)市場對口罩的需求量<(百萬個)與天數(shù)![]() 呈拋物線型,第
呈拋物線型,第![]() 天市場口罩缺口(需求量與供應(yīng)量差)就達到
天市場口罩缺口(需求量與供應(yīng)量差)就達到![]() (百萬個),之后若干天,市場口罩需求量不斷上升,在第
(百萬個),之后若干天,市場口罩需求量不斷上升,在第![]() 天需求量達到最高峰
天需求量達到最高峰![]() (百萬個).
(百萬個).
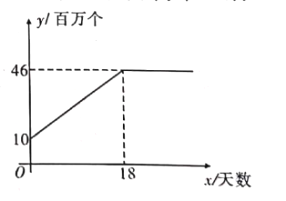
![]() 求出
求出![]() 與
與![]() 的函數(shù)解析式;
的函數(shù)解析式;
![]() 當市場供應(yīng)量不小于需求量時,市民買口罩才無需提前預(yù)約,那么在整個二月份,市民無需預(yù)約即可購買口罩的天數(shù)共有多少天?
當市場供應(yīng)量不小于需求量時,市民買口罩才無需提前預(yù)約,那么在整個二月份,市民無需預(yù)約即可購買口罩的天數(shù)共有多少天?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,BC是⊙O的切線,D是⊙O上的一點,且AD//CO.

(1)求證:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的長.(結(jié)果保留根號)
,求AD的長.(結(jié)果保留根號)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com