
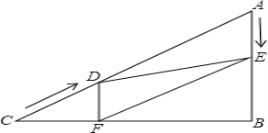
【題目】如圖,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,點D從點C出發沿CA方向以4cm/秒的速度向點A勻速運動,同時點E從點A出發沿AB方向以2cm/秒的速度向點B勻速運動,當其中一個動點到達終點時,另一個動點也隨之停止運動.設點D、E運動的時間是t秒(0<t≤15).過點D作DF⊥BC于點F,連接DE,EF.
(1)當t為何值時,DF=DA?
(2)當t為何值時,△ADE為直角三角形?請說明理由.
(3)是否存在某一時刻t,使點F在線段AC的中垂線上,若存在,請求出t值,若不存在,請說明理由.
(4)請用含有t式子表示△DEF的面積,并判斷是否存在某一時刻t,使△DEF的面積是△ABC面積的![]() ,若存在,請求出t值,若不存在,請說明理由.
,若存在,請求出t值,若不存在,請說明理由.
【答案】(1)10;(2)t=![]() 或12,理由見解析;(3) t=10,理由見解析;(4)
或12,理由見解析;(3) t=10,理由見解析;(4)![]()
【解析】
(1) 由已知條件可得Rt△CDF中∠C=30°,即可知DF=![]() CD=AE=2t,列方程求解即可;
CD=AE=2t,列方程求解即可;
(2)分兩種情況討論即可求解;
(3)假設存在,再根據垂直平分線的性質求解即可;
(4)利用兩個三角形的面積關系求解即可.
(1)證明:由題意得:AE=2t,CD=4t,
∵DF⊥BC∴∠CFD=90°,
∵∠C=90°-60°=30°,
∴DF=![]() CD=2t,
CD=2t,
同理:AB=![]() AC=30cm
AC=30cm
若:DF=DA,則:2t=60-4t,
解得: t=10;
(2) 當∠AED=90°時,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE 即60-4t=4t,
解得:t=![]()
當∠ADE=90°時,
∵∠A=60°, ∴∠DEA=30°,
∴AD=![]() AE
AE
∴60-4t=t 解得t=12.
(3)連接AF,
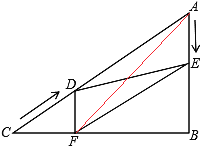
若存在,則CF=AF,
∴∠C=∠CAF=30°
∴∠AFB=60°
∴∠FAB=30°
RT△DCF中,有勾股定理得:CF=![]()
同理:BC=![]()
∴FB=![]() AF=
AF=![]() =
=![]()
解得:t=10.
(4)![]()
∴![]()
∴![]()
若存在,則![]()
解得![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
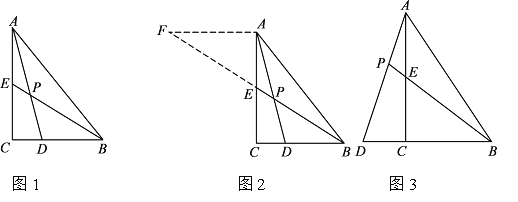
小昊遇到這樣一個問題:如圖1,在△ABC中,∠ACB=90°,BE是AC邊上的中線,點D在BC邊上,CD:BD=1:2,AD與BE相交于點P,求![]() 的值.
的值.
小昊發現,過點A作AF∥BC,交BE的延長線于點F,通過構造△AEF,經過推理和計算能夠使問題得到解決(如圖2).請回答:![]() 的值為 .
的值為 .
參考小昊思考問題的方法,解決問題:
如圖 3,在△ABC中,∠ACB=90°,點D在BC的延長線上,AD與AC邊上的中線BE的延長線交于點P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,則BP=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校將進行“校春季運動會”,現從全校學生中選出![]() 名同學參加運動會相關服務工作,其中
名同學參加運動會相關服務工作,其中![]() 名男生,
名男生,![]() 名女生.
名女生.
(1)若從這![]() 名同學中隨機選取
名同學中隨機選取![]() 人作為聯絡員,求選到男生的概率.
人作為聯絡員,求選到男生的概率.
(2)若運動會的某項服務工作只在![]() ,
,![]() 兩位同學中選一人,準備用游戲的方式決定誰參加.游戲規則是:四個乒乓球上的數字分別為
兩位同學中選一人,準備用游戲的方式決定誰參加.游戲規則是:四個乒乓球上的數字分別為![]() ,
,![]() ,
,![]() ,
,![]() (乒乓球只有數字不同,其余完全相同),將乒乓球放在不透明的紙箱中,從中任意摸取兩個,若取到的兩個乒乓球上的數字之和大于
(乒乓球只有數字不同,其余完全相同),將乒乓球放在不透明的紙箱中,從中任意摸取兩個,若取到的兩個乒乓球上的數字之和大于![]() 則選
則選![]() ,否則選
,否則選![]() ,從是否公平的角度看,該游戲規則是否合理,用樹狀圖或表格說明理由.
,從是否公平的角度看,該游戲規則是否合理,用樹狀圖或表格說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E、F、G、H分別是BD、BC、AC、AD的中點,且AB=CD.下列結論:①EG⊥FH,②四邊形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四邊形EFGH是菱形.其中正確的個數是 ( )
(BC-AD),⑤四邊形EFGH是菱形.其中正確的個數是 ( )
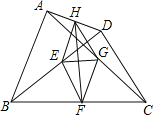
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第十五屆中國“西博會”將于2014年10月底在成都召開,現有20名志愿者準備參加某分會場的工作,其中男生8人,女生12人.
(1)若從這20人中隨機選取一人作為聯絡員,求選到女生的概率;
(2)若該分會場的某項工作只在甲、乙兩人中選一人,他們準備以游戲的方式決定由誰參加,游戲規則如下:將四張牌面數字分別為2、3、4、5的撲克牌洗勻后,數字朝下放于桌面,從中任取2張,若牌面數字之和為偶數,則甲參加,否則乙參加.試問這個游戲公平嗎?請用樹狀圖或列表法說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為進一步深化基教育課程改革,構建符合素質教育要求的學校課程體系,某學校自主開發了A書法、B閱讀,C足球,D器樂四門校本選修課程供學生選擇,每門課程被選到的機會均等.
(1)學生小紅計劃選修兩門課程,請寫出所有可能的選法;
(2)若學生小明和小剛各計劃送修一門課程,則他們兩人恰好選修同一門課程的概率為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,點D在AB邊上(不與點A、B重合),以CD為腰作等腰直角
,點D在AB邊上(不與點A、B重合),以CD為腰作等腰直角![]() ,
,![]() .
.
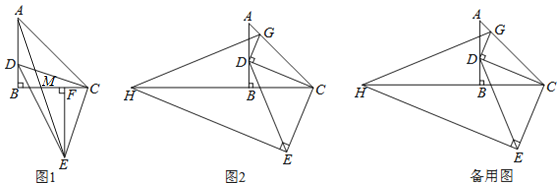
(1)如圖1,作![]() 于F,求證:
于F,求證:![]() ;
;
(2)在圖1中,連接AE交BC于M,求![]() 的值。
的值。
(3)如圖2,過點E作![]() 交CB的延長線于點H,過點D作
交CB的延長線于點H,過點D作![]() ,交AC于點G,連接GH當點D在邊AB上運動時,式子
,交AC于點G,連接GH當點D在邊AB上運動時,式子![]() 的值會發生變化嗎?若不變,求出該值:若變化請說明理由.
的值會發生變化嗎?若不變,求出該值:若變化請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
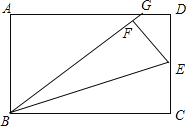
【題目】如圖,在矩形ABCD中,點E是CD的中點,將△BCE沿BE折疊后得到△BEF、且點F在矩形ABCD的內部,將BF延長交AD于點G.若![]() ,則
,則![]() =__.
=__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于任意一個三位數![]() ,將它任意兩個數位上的數字對調后得到一個首位不為0的新的三位數
,將它任意兩個數位上的數字對調后得到一個首位不為0的新的三位數![]() (
(![]() 可以與
可以與![]() 相同),記
相同),記![]() ,在所有可能的情況中,當
,在所有可能的情況中,當![]() 最小時,我們稱此時的
最小時,我們稱此時的![]() 是
是![]() 的“平安快樂數”,并規定
的“平安快樂數”,并規定![]() .例如:318按上述方法可得新數381、813、138,因為
.例如:318按上述方法可得新數381、813、138,因為![]() ,
,![]() ,
,![]() ,而
,而![]() ,所以138是318的“平安快樂數”,此時
,所以138是318的“平安快樂數”,此時![]() .
.
(1)168的“平安快樂數”為_______________,![]() ______________;
______________;
(2)若![]() (
(![]() ,
,![]() 都是正整數),交換其十位與百位上的數字得到新數
都是正整數),交換其十位與百位上的數字得到新數![]() ,當
,當![]() 是13的倍數時,求
是13的倍數時,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com