
【題目】如果方程x2+px+q=0的兩個根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,請根據以上結論,解決下列問題:
(1)若p=﹣4,q=3,求方程x2+px+q=0的兩根.
(2)已知實數a、b滿足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 ![]() +
+ ![]() 的值;
的值;
(3)已知關于x的方程x2+mx+n=0,(n≠0),求出一個一元二次方程,使它的兩個根分別是已知方程兩根的倒數.
【答案】
(1)解:當p=﹣4,q=3,則方程為x2﹣4x+3=0,
解得:x1=3,x2=1
(2)解:∵a、b滿足a2﹣15a﹣5=0,b2﹣15b﹣5=0,
∴a、b是x2﹣15x﹣5=0的解,
當a≠b時,a+b=15,a﹣b=﹣5,
![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() =﹣47;
=﹣47;
當a=b時,原式=2
(3)解:設方程x2+mx+n=0,(n≠0),的兩個根分別是x1,x2,
則 ![]() +
+ ![]() =
= ![]() =﹣
=﹣ ![]() ,
, ![]()
![]() =
= ![]() =
= ![]() ,
,
則方程x2+ ![]() x+
x+ ![]() =0的兩個根分別是已知方程兩根的倒數
=0的兩個根分別是已知方程兩根的倒數
【解析】(1)根據p=﹣4,q=3,得出方程x2﹣4x+3=0,再求解即可;(2)根據a、b滿足a2﹣15a﹣5=0,b2﹣15b﹣5=0,得出a,b是x2﹣15x﹣5=0的解,求出a+b和ab的值,即可求出 ![]() +
+ ![]() 的值;(3)先設方程x2+mx+n=0,(n≠0)的兩個根分別是x1 , x2 , 得出
的值;(3)先設方程x2+mx+n=0,(n≠0)的兩個根分別是x1 , x2 , 得出 ![]() +
+ ![]() =﹣
=﹣ ![]() ,
, ![]()
![]() =
= ![]() ,再根據這個一元二次方程的兩個根分別是已知方程兩根的倒數,即可求出答案.
,再根據這個一元二次方程的兩個根分別是已知方程兩根的倒數,即可求出答案.
【考點精析】通過靈活運用根與系數的關系,掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系數a、b、c而定;兩根之和等于方程的一次項系數除以二次項系數所得的商的相反數;兩根之積等于常數項除以二次項系數所得的商即可以解答此題.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】在開展“學雷鋒社會實踐”活動中,某校為了解全校1200名學生參加活動的情況,隨機調查了50名學生每人參加活動的次數,并根據數據繪成條形統計圖如圖. 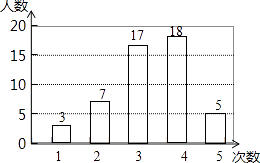
(Ⅰ)求這50個樣本數據的平均數、眾數和中位數;
(Ⅱ)根據樣本數據,估算該校1200名學生共參加了多少次活動?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算與解方程
(1)計算: ![]() ﹣(
﹣( ![]() +1)﹣1+(
+1)﹣1+( ![]() ﹣
﹣ ![]() )0
)0
(2)用適當的方法解下列方程: ①x2﹣12x﹣4=0;
②(x﹣1)2+2x(x﹣1)=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
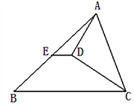
【題目】如圖,在△ABC中,從A點向∠ACB的角平分線作垂線,垂足為D,E是AB的中點,已知AC=4,BC=6,則DE的長為( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請寫出滿足下列條件的一個不等式.
(1)0是這個不等式的一個解:;
(2)﹣2,﹣1,0,1都是不等式的解:;
(3)0不是這個不等式的解:;
(4)與X≤﹣1的解集相同的不等式: .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com