Question

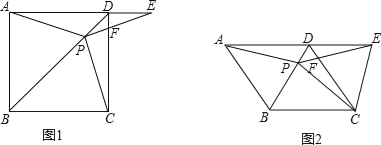
【題目】如圖1，在正方形ABCD中，P是對角線BD上的一點，點E在AD的延長線上，且PA=PE，PE交CD于F．

（1）證明：PC=PE；

（2）求∠CPE的度數；

（3）如圖2，把正方形ABCD改為菱形ABCD，其他條件不變，當∠ABC=120°時，連接CE，試探究線段AP與線段CE的數量關系，并說明理由．

Answer 1

【答案】（1）證明見解析（2）90°（3）AP=CE

【解析】

試題(1)、根據正方形得出AB=BC，∠ABP=∠CBP=45°，結合PB=PB得出△ABP ≌△CBP，從而得出結論；(2)、根據全等得出∠BAP=∠BCP，∠DAP=∠DCP，根據PA=PE得出∠DAP=∠E，即∠DCP=∠E，然后根據180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E得出答案；(3)、首先證明△ABP和△CBP全等，然后得出PA=PC，∠BAP=∠BCP，然后得出∠DCP=∠E，從而得出∠CPF=∠EDF=60°，然后得出△EPC是等邊三角形，從而得出AP=CE.

試題解析：(1)、在正方形ABCD中，AB=BC，∠ABP=∠CBP=45°，

在△ABP和△CBP中，又∵ PB=PB ∴△ABP ≌△CBP（SAS）， ∴PA=PC，∵PA=PE，∴PC=PE；

(2)、由（1）知，△ABP≌△CBP，∴∠BAP=∠BCP，∴∠DAP=∠DCP，

∵PA=PE， ∴∠DAP=∠E， ∴∠DCP=∠E， ∵∠CFP=∠EFD（對頂角相等），

∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E， 即∠CPF=∠EDF=90°；

(3)、AP＝CE

理由是：在正方形ABCD中，AB=BC，∠ABP=∠CBP=45°，

在△ABP和△CBP中， 又∵ PB=PB ∴△ABP≌△CBP（SAS）， ∴PA=PC，∠BAP=∠BCP，

∵PA=PE，∴PC=PE，∴∠DAP=∠DCP， ∵PA=PC ∴∠DAP=∠E， ∴∠DCP=∠E

∵∠CFP=∠EFD（對頂角相等）， ∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E，

即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°， ∴△EPC是等邊三角形，∴PC=CE，∴AP=CE