Question

【題目】如圖（1），菱形ABCD對角線AC、BD的交點O是四邊形EFGH對角線FH的中點，四個頂點A、B、C、D分別在四邊形EFGH的邊EF、FG、GH、HE上．

（1）求證：四邊形EFGH是平行四邊形；

（2）如圖（2）若四邊形EFGH是矩形，當AC與FH重合時，已知，且菱形ABCD的面積是20，求矩形EFGH的長與寬．

Answer 1

【答案】(1)證明過程見解析；(2)長為8，寬為4.

【解析】

試題分析：(1)、根據菱形的性質可得出OA=OC，OD=OB，再由中點的性質可得出OF=OH，結合對頂角相等即可利用全等三角形的判定定理（SAS）證出△AOF≌△COH，從而得出AF∥CH，同理可得出DH∥BF，依據平行四邊形的判定定理即可證出結論；(2)、設矩形EFGH的長為a、寬為b．根據勾股定理及邊之間的關系可找出AC=，BD=，利用菱形的性質、矩形的性質可得出∠AOB=∠AGH=90°，從而可證出△BAO∽△CAG，根據相似三角形的性質可得出，套入數據即可得出a=2b①，再根據菱形的面積公式得出a2+b2=80②，聯立①②解方程組即可得出結論．

試題解析：(1)/∵點O是菱形ABCD對角線AC、BD的交點， ∴OA=OC，OD=OB，

∵點O是線段FH的中點， ∴OF=OH．

在△AOF和△COH中，有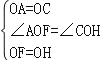， ∴△AOF≌△COH（SAS）， ∴∠AFO=∠CHO， ∴AF∥CH．

同理可得：DH∥BF． ∴四邊形EFGH是平行四邊形．

(2)、設矩形EFGH的長為a、寬為b，則AC=． ∵=2，

∴BD=AC=，OB=BD=，OA=AC=．

∵四邊形ABCD為菱形， ∴AC⊥BD， ∴∠AOB=90°． ∵四邊形EFGH是矩形， ∴∠AGH=90°，

∴∠AOB=∠AGH=90°， 又∵∠BAO=∠CAG， ∴△BAO∽△CAG，

∴，即， 解得：a=2b①．

∵S菱形ABCD=ACBD==20， ∴a2+b2=80②．

聯立①②解得：，或（舍去）．

∴矩形EFGH的長為8，寬為4．