
【題目】如圖,在梯形![]() 中,
中,![]() ,
,![]() 交邊
交邊![]() 于點
于點![]() .
.

(1)當點![]() 與
與![]() 恰好重合時(如圖1),求
恰好重合時(如圖1),求![]() 的長;
的長;
(2)問:是否可能使![]() 、
、![]() 與
與![]() 都相似?若能,請求出此時
都相似?若能,請求出此時![]() 的長;若不能,請說明理由(如圖2).
的長;若不能,請說明理由(如圖2).
【答案】(1)2;(2)AD =2![]() .
.
【解析】
(1)由∠DCA=∠CAB,∠ADC=∠ACB,證得△ACD∽△ABC,利用相似三角形的對應邊成比例,即可求得AD的長;
(2)分別從使△ABE、△CDE與△BCE都相似分析,利用相似三角形的性質,即可求得AD的長.
解:(1)當點E與A重合時,∵CD∥AB,
∴∠DCA=∠CAB,且∠ADC=∠ACB=90°,
∴△ACD∽△ABC,
∴![]() ,
,
∴AC=2![]() ,
,
∴AD=![]() .
.
(2)若能使△ABE、△CDE與△BCE都相似,
∴∠EBC=∠A=∠D=90°,∠DEC=∠BEC=∠AEB,
∵∠DEC+∠BEC+∠AEB=180,
∴∠DEC=∠BEC=∠AEB=60°.
在Rt△DEC中,tan∠DEC=![]() ,
,
∴DE=![]() .
.
在Rt△ABE中,tan∠AEB=![]() ,
,
∴EA=![]() ,
,
∴AD=DE+AE=2![]() .
.


科目:初中數學 來源: 題型:
【題目】泉州市旅游資源豐富,①清源山、②開元寺、③崇武古城三個景區是人們節假日玩的熱點景區,張老師對八(1)班學生“五·一”小長假隨父母到這三個景區游玩的計劃做了全面調查,調查分四個類別:A、游三個景區;B,游兩個景區;C,游一個景區:D,不到這三個景區游玩現根據調查結果繪制了不完整的條形統計圖和廟形統計圖,請結合圖中信息解答下列問題:
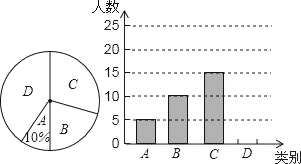
(1)八(1)班共有學生 人在扇形統計圖中,表示“B類別的扇形的圓心角的度數為 ;
(2)請將條形統計圖補充完整;
(3)若小華、小剛兩名同學,各自從三個最區中隨機選一個作為5月1日游玩的景區,請用樹狀圖或列表法求他們選中同個景區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實踐與探究
在平面直角坐標系中,四邊形AOBC是矩形,點![]() (0,0),點A(5,0),點B(0,3).以點A為中心,順時針旋轉矩形AOBC,得到矩形ADEF,點O,B,C的對應點分別為D,E,F.
(0,0),點A(5,0),點B(0,3).以點A為中心,順時針旋轉矩形AOBC,得到矩形ADEF,點O,B,C的對應點分別為D,E,F.
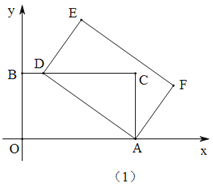
(1)如圖(1),當點D落在BC邊上時,求點D的坐標;
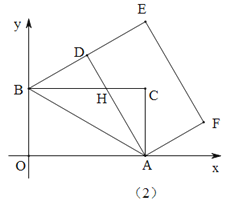
(2)如圖(2),當點D落在線段BE上時,AD與BC交于點H.
①求證:ΔADB≌ΔAOB;
②求點H的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品的進價為每件![]() 元,現在的售價為每件
元,現在的售價為每件![]() 元,每星期可賣出
元,每星期可賣出![]() 件.市場調查反映:如果每件的售價每漲
件.市場調查反映:如果每件的售價每漲![]() 元(售價每件不能高于
元(售價每件不能高于![]() 元),那么每星期將少賣出
元),那么每星期將少賣出![]() 件.設每件漲價
件.設每件漲價![]() 元(
元(![]() 為非負整數),每星期的銷量為
為非負整數),每星期的銷量為![]() 件.
件.
①求![]() 與
與![]() 的函數關系式及自變量
的函數關系式及自變量![]() 的取值范圍;
的取值范圍;
②如何定價才能使每星期的利潤最大?每星期的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把某矩形紙片ABCD沿EF,GH折疊(點E,H在AD邊上,點F,G在BC邊上),使點B和點C落在AD邊上同一點P處,A點的對稱點為A′點,D點的對稱點為D′點,若∠FPG=90°,△A′EP的面積為5,△D′PH的面積為20,則矩形ABCD的面積等于_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
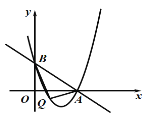
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,拋物線經過
,拋物線經過![]() 、
、![]() 兩點,且對稱軸為直線
兩點,且對稱軸為直線![]() .
.
(1)求拋物線的表達式;
(2)如果點![]() 是這拋物線上位于
是這拋物線上位于![]() 軸下方的一點,且△
軸下方的一點,且△![]() 的面積是
的面積是![]() .求點
.求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義符號min{a,b}的含義為:當a≥b時,min{a,b}=b;當a<b時,min{a,b}=a,如:min{1,-2)=-2,min{-3,-2)=-3,則方程min{x,-x}=x2-1的解是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ACB中,∠C=90°,點D在AC上,∠CBD=∠A,過A、D兩點的圓的圓心O在AB上.
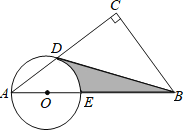
(1)判斷BD所在直線與⊙O的位置關系,并證明你的結論;
(2)若AE=4,∠A=30°,求圖中由BD、BE、弧DE圍成陰影部分面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com