
【題目】如圖,拋物線y=ax2+bx+c的對稱軸是x=﹣1,且過點(![]() ,0),有下列結論:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有錯誤的結論有( )個.
,0),有下列結論:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有錯誤的結論有( )個.
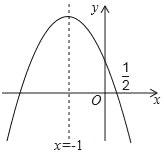
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
根據拋物線的開口方向、對稱軸、與y軸的交點判定系數符號,及運用一些特殊點解答問題.
由拋物線的開口向下可得:a<0,
根據拋物線的對稱軸在y軸左邊可得:a,b同號,所以b<0,
根據拋物線與y軸的交點在正半軸可得:c>0,
∴abc>0,故①正確;
直線x=﹣1是拋物線y=ax2+bx+c(a≠0)的對稱軸,所以﹣![]() =﹣1,可得b=2a,
=﹣1,可得b=2a,
a﹣2b+4c=a﹣4a+4c=﹣3a+4c,
∵a<0,
∴﹣3a>0,
∴﹣3a+4c>0,
即a﹣2b+4c>0,故②錯誤;
∵拋物線y=ax2+bx+c的對稱軸是x=﹣1.且過點(![]() ,0),
,0),
∴拋物線與x軸的另一個交點坐標為(﹣![]() ,0),
,0),
當x=﹣![]() 時,y=0,即a(﹣
時,y=0,即a(﹣![]() )2+b×(﹣
)2+b×(﹣![]() )+c=0,
)+c=0,
整理得:25a﹣10b+4c=0,故③正確;
∵b=2a,a+b+c<0,
∴![]() b+b+c<0,
b+b+c<0,
即3b+2c<0,故④錯誤;
∵x=﹣1時,函數值最大,
∴a﹣b+c>m2a﹣mb+c(m≠﹣1),
∴a﹣b>m(am﹣b),所以⑤正確;
故選:B.


科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣![]() x2+bx+c經過點(1,0),(0,
x2+bx+c經過點(1,0),(0,![]() ).
).
(1)求該拋物線的函數表達式;
(2)將拋物線y=﹣![]() x2+bx+c平移,使其頂點恰好落在原點,請寫出一種平移的方法及平移后的函數表達式.
x2+bx+c平移,使其頂點恰好落在原點,請寫出一種平移的方法及平移后的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:①b2﹣4ax>0;②2a+b>0;③abc<0;④4a﹣2b+c<0;⑤a+b+c>0.其中正確的個數是( )
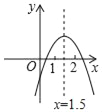
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動小組的同學為測量旗桿高度,先制定了如下測量方案,使用工具是測角儀和皮尺,請幫助組長林平完成方案內容,用含a,b,α的代數式表示旗桿AB的高度.
數學活動方案
活動時間:2018年4月2日 活動地點:學校操場 填表人:林平
課題 | 測量學校旗桿的高度 | ||
活動目的 | 運用所學數學知識及方法解決實際問題 | ||
方案示意圖 |
| 測量步驟 | (1)用什么測得∠ADE=α; (2)用什么測得BC=a米,CD=b米. |
(3)計算過程 | |||
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在四張背面完全相同的紙牌的正面分別畫有四個不同的幾何圖形,將這四張紙牌背面朝上洗勻后摸出一張,不放回,再摸出一張
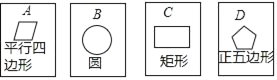
(1)用樹狀圖(或列表法)表示兩次摸牌所有可能出現的結果(紙牌可用A、B、C、D表示);
(2)求摸出的兩張紙牌牌面上所畫幾何圖形既是軸對稱圖形又是中心對稱圖形的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖1,在ABCD中,點E是AB中點,連接DE并延長,交CB的延長線于點F.
(1)求證:△ADE≌△BFE;
(2)如圖2,點G是邊BC上任意一點(點G不與點B、C重合),連接AG交DF于點H,連接HC,過點A作AK∥HC,交DF于點K.
①求證:HC=2AK;
②當點G是邊BC中點時,恰有HD=nHK(n為正整數),求n的值.
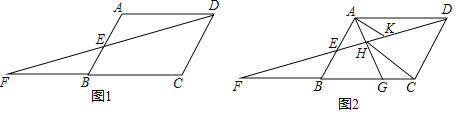
查看答案和解析>>
科目:初中數學 來源: 題型:
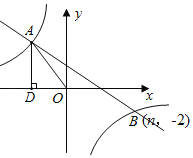
【題目】如圖所示,在平面直角坐標系中,一次函數y=kx+b(k≠0)與反比例函數y=![]() (m≠0)的圖象交于第二、四象限A、B兩點,過點A作AD⊥x軸于D,AD=4,sin∠AOD=
(m≠0)的圖象交于第二、四象限A、B兩點,過點A作AD⊥x軸于D,AD=4,sin∠AOD=![]() ,且點B的坐標為(n,-2).
,且點B的坐標為(n,-2).
(1)求一次函數與反比例函數的解析式;
(2)E是y軸上一點,且△AOE是等腰三角形,請直接寫出所有符合條件的E點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年(1)班的體育課上,小明、小強和小華三人在學習訓練足球,足球從一人傳到另一人就記為踢一次.
(1)如果從小強開始踢,經過兩次踢球后,足球踢到了小明處的概率是多少?請用數狀圖或列表法說明.
(2)如果踢三次,球踢到了小明處的可能性最小,應從誰開始踢?(直接寫出結論)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com