Question

【題目】我們知道：垂直于弦的直徑平分這條弦，并且平分這條弦所對的兩條弧；平分弧的直徑垂直平分這條弧所對的弦．你可以利用這一結論解決問題：
如圖，點P在以MN（南北方向）為直徑的⊙O上，MN=8，PQ⊥MN交⊙O于點Q，垂足為H，PQ≠MN，弦PC、PD分別交MN于點E、F，且PE=PF．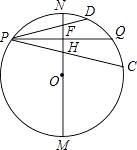

（1）比較 與 的大小；
（2）若OH=2 ，求證：OP∥CD；
（3）設直線MN、CD相交所成的銳角為α，試確定cosα= 時，點P的位置．

Answer 1

【答案】
（1）解：∵PE=PF，PH⊥EF，

∴PH平分∠FPE，

∴∠DPQ=∠CPQ，

∴ = ；

（2）證明：連結CD、OP、OQ，OQ交CD于B，如圖，

∵OH=2 ，OP=4，

∴PH= =2 ，

∴△OPH為等腰直角三角形，

∴∠OPQ=45°，

而OP=OQ，

∴△OPQ為等腰直角三角形，

∴∠POQ=90°，

∴OP⊥OQ，

∵ = ，

∴OQ⊥CD，

∴OP∥CD

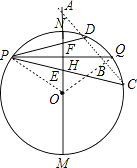
（3）解：直線CD交MN于A，如圖，

∵cosα= ，

∴∠α=30°，即直線MN、CD相交所成的銳角為30°，

而OB⊥CD，

∴∠AOB=60°，

∵OH⊥PQ，

∴∠POH=60°，

在Rt△POH中，∵sin∠POH= ，

∴PH=4sin60°=2 ，

即點P到MN的距離為2 ．

【解析】（1）根據等腰三角形的性質，由PE=PF，PH⊥EF可判斷PH平分∠FPE，然后根據圓中角定理得到 = ；（2）連結CD、OP、OQ，OQ交CD于B，如圖，先計算出PH=2 ，則可判斷△OPH為等腰直角三角形得到∠OPQ=45°，再判斷△OPQ為等腰直角三角形得到∠POQ=90°，然后根據垂徑的推理由 = 得到OQ⊥CD，則根據平行線的判定方法得OP∥CD；（3）直線CD交MN于A，如圖，由特殊角的三角函數值得∠α=30°，即直線MN、CD相交所成的銳角為30°，利用OB⊥CD得到∠AOB=60°，則∠POH=60°，然后在Rt△POH中利用正弦的定義計算出PH即可．本題考查了圓的綜合題：熟練掌握垂徑定理及其推理、圓周角定理；能夠靈活應用等腰直角三角形的性質和三角函數進行幾何計算．