【題目】如圖，半圓O的直徑AB=10cm，弦AC=6cm，AD平分∠BAC，則AD的長為（ ） 
A.
cm
B.
cm
C.
cm
D.4cm
【答案】A
【解析】解：連接OD，OC，作DE⊥AB于E，OF⊥AC于F， 
∵∠CAD=∠BAD（角平分線的性質），
∴ 
，
∴∠DOB=∠OAC=2∠BAD，
∴△AOF≌△ODE，
∴OE=AF= 
AC=3（cm），
在Rt△DOE中，DE= 
=4（cm），
在Rt△ADE中，AD= 
=4 
（cm）．
故選：A．
【考點精析】根據題目的已知條件，利用勾股定理的概念和圓心角、弧、弦的關系的相關知識可以得到問題的答案，需要掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2；在同圓或等圓中，相等的圓心角所對的弧相等，所對的弦也相等；在同圓或等圓中，同弧等弧所對的圓周角相等，都等于這條弧所對的圓心角的一半．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，在ABCD中，點O是邊BC的中點，連接DO并延長，交AB延長線于點E，連接BD，EC．
（1）求證：四邊形BECD是平行四邊形；
（2）若∠A=50°，則當∠BOD= ______ °時，四邊形BECD是矩形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,將一張長方形紙片分別沿著EP,FP對折，使B落在B′，C落在C′．
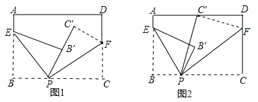
（1）若點P,B′,C′在同一直線上(圖1），求兩條折痕的夾角∠EPF的度數；
（2）若點P,B′,C′不在同一直線上(圖2），且∠B′PC′=10°，求∠EPF的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，⊙O的半徑OD⊥弦AB于點C，連結AO并延長交⊙O于點E，連結EC．若AB=8，CD=2，則EC的長為（ ） 
A.2 
B.8
C.2 
D.2 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一點，將Rt△ABC沿CD折疊，使B點落在AC邊上的B′處，則∠CDB′等于（ ）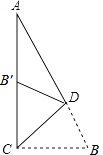 
A.40°
B.60°
C.70°
D.80°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在△ABC中，∠ABC=90°，AB=3，BC=4．點Q是線段AC上的一個動點，過點Q作AC的垂線交線段AB（如圖1）或線段AB的延長線（如圖2）于點P． 
（1）當點P在線段AB上時，求證：△AQP∽△ABC；
（2）當△PQB為等腰三角形時，求AP的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
