
【題目】如圖1,已知點![]() 、
、![]() 在直線
在直線![]() 上,且
上,且![]() ,
,![]() 于
于![]() 點,且
點,且![]() ,以
,以![]() 為直徑在
為直徑在![]() 的左側作半圓
的左側作半圓![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,
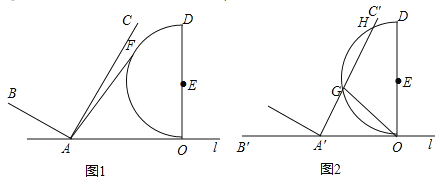
(1)若半圓![]() 上有一點
上有一點![]() ,則
,則![]() 的最大值為__________,最小值為__________;
的最大值為__________,最小值為__________;
(2)向右沿直線![]() 平移
平移![]() 得到
得到![]() ;
;
①如圖2,若![]() 截半圓
截半圓![]() 的弧
的弧![]() 的長為
的長為![]() ,求
,求![]() 的度數;
的度數;
②當半圓![]() 與
與![]() 的邊相切時,求平移距離.
的邊相切時,求平移距離.
【答案】(1)![]() ,
,![]() ;(2)①75°;②
;(2)①75°;②![]() 或
或![]() .
.
【解析】
(1)當![]() 和
和![]() 重合時,
重合時,![]() 最大,用勾股定理可求;連接
最大,用勾股定理可求;連接![]() ,此時
,此時![]() 最小,為
最小,為![]() ;
;
(2)①連接![]() ,
,![]() ,依據弧長公式,求出
,依據弧長公式,求出![]() ,證得
,證得![]() 是等邊三角形,求出
是等邊三角形,求出![]() ,得出
,得出![]() ,依據平行線的判定及性質求出
,依據平行線的判定及性質求出![]() ,依據等腰直角三角形的性質求出
,依據等腰直角三角形的性質求出![]() ,最后求得
,最后求得![]() ;
;
②分![]() 、
、![]() 分別與半圓
分別與半圓![]() 相切兩種情況討論,依據切線的性質與判定、切線長定理、銳角三角函數求解即可.
相切兩種情況討論,依據切線的性質與判定、切線長定理、銳角三角函數求解即可.
解:(1)當![]() 和
和![]() 重合時,
重合時,![]() 的最大值為
的最大值為![]() ,由勾股定理計算得
,由勾股定理計算得![]() ,
,
連接![]() ,此時
,此時![]() 最小,為
最小,為![]() =
=![]() ;
;
故答案為:![]() ,
,![]() ;
;
(2)①連接![]() ,
,![]() ,
,
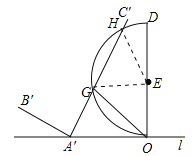
∵弧![]() 的長為
的長為![]()
∴![]()
又∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
②當![]() 切半圓
切半圓![]() 于
于![]() 時,連接
時,連接![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() 切半圓
切半圓![]() 于
于![]() 點,
點,
∴![]()
又∵![]() ,
,
∴![]() ,
,
平移距離為![]()
當![]() 切半圓
切半圓![]() 于
于![]() 時,連接
時,連接![]() 并延長交
并延長交![]() 于
于![]() 點,
點,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ,
,
∴平移距離為![]() .
.
綜上所述:平移距離為![]() 或
或![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
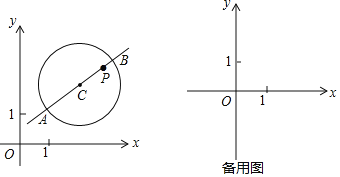
【題目】在平面直角坐標系xOy中,⊙C的半徑為r(r>1),P是圓內與圓心C不重合的點,⊙C的“完美點”的定義如下:若直線CP與⊙C交于點A,B,滿足|PA﹣PB|=2,則稱點P為⊙C的“完美點”,如圖為⊙C及其“完美點”P的示意圖.
(1)當⊙O的半徑為2時,
①在點M![]() ,N(0,1),T
,N(0,1),T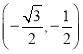 中,⊙O的“完美點”是 ;
中,⊙O的“完美點”是 ;
②若⊙O的“完美點”P在直線y=![]() x上,求PO的長及點P的坐標;
x上,求PO的長及點P的坐標;
(2)⊙C的圓心在直線y=![]() x+1上,半徑為2,若y軸上存在⊙C的“完美點”,求圓心C的縱坐標t的取值范圍.
x+1上,半徑為2,若y軸上存在⊙C的“完美點”,求圓心C的縱坐標t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
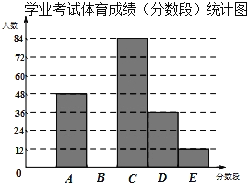
【題目】為了解某市九年級學生學業考試體育成績,現從中隨機抽取部分學生的體育成績進行分段(A:50分;B:49﹣45分;C:44﹣40分;D:39﹣30分;E:29﹣0分)統計如下:
學業考試體育成績(分數段)統計表
分數段 | 人數(人) | 頻率 |
A | 48 | 0.2 |
B | a | 0.25 |
C | 84 | 0.35 |
D | 36 | b |
E | 12 | 0.05 |
根據上面提供的信息,回答下列問題:
(1)在統計表中,a的值為 ,b的值為 ,并將統計圖補充完整(溫馨提示:作圖時別忘了用0.5毫米及以上的黑色簽字筆涂黑);
(2)甲同學說:“我的體育成績是此次抽樣調查所得數據的中位數.”請問:甲同學的體育成績應在什么分數段內? (填相應分數段的字母)
(3)如果把成績在40分以上(含40分)定為優秀,那么該市今年10440名九年級學生中體育成績為優秀的學生人數約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:![]() 中,
中,![]() ,求證:
,求證:![]() ,下面寫出可運用反證法證明這個命題的四個步驟:
,下面寫出可運用反證法證明這個命題的四個步驟:
①∴![]() ,這與三角形內角和為
,這與三角形內角和為![]() 矛盾,②因此假設不成立.∴
矛盾,②因此假設不成立.∴![]() ,③假設在
,③假設在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .這四個步驟正確的順序應是( )
.這四個步驟正確的順序應是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,對角線AC,BD交于點O,且AC⊥BC,點E是BC延長線上一點, ![]() ,連接DE.
,連接DE.
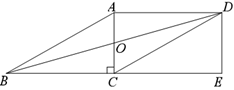
(1)求證:四邊形ACED為矩形;
(2)連接OE,如果BD=10,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系內,已知點A的坐標為(-6,0),直線l:y=kx+b不經過第四象限,且與x軸的夾角為30°,點P為直線l上的一個動點,若點P到點A的最短距離是2,則b的值為( )
A. ![]() 或
或![]() B.
B. ![]() C. 2
C. 2![]() D. 2
D. 2![]() 或10
或10![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
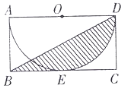
【題目】如圖,在矩形ABCD中,BC=2,CD=1,以AD為直徑的半圓O與BC相切于點E,連接BD,則陰影部分的面積為__________.(結果保留![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(﹣4,8)和點B(2,n)在拋物線y=ax2上.
(Ⅰ)求該拋物線的解析式和頂點坐標,并求出n的值;
(Ⅱ)求點B關于x軸對稱點P的坐標,并在x軸上找一點Q,使得AQ+QB最短,求此時點Q的坐標;
(Ⅲ)平移拋物線y=ax2,記平移后點A的對應點為A',點B的對應點為B',點C(﹣2,0)是x軸上的定點.
①當拋物線向左平移到某個位置時,A'C+CB'最短,求此時拋物線的解析式;
②D(﹣4,0)是x軸上的定點,當拋物線向左平移到某個位置時,四邊形A'B'CD的周長最短,求此時拋物線的解析式(直接寫出結果即可).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com