
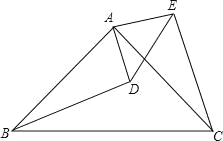
【題目】如圖,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°
(1)求證:CE=BD;
(2)求證:CE⊥BD.
【答案】(1)、證明過程見解析;(2)、證明過程見解析.
【解析】
試題分析:(1)、由已知條件證出∠CAE=∠BAD,由SAS證明△CAE≌△BAD,得出對應邊相等即可;
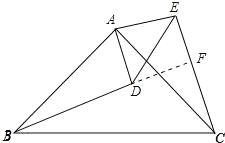
(2)、延長BD交CE于F,由全等三角形的性質得出∠ACE=∠ABD,由角的互余關系得出∠ABC+∠ACB=90°,證出∠DBC+∠BCF=90°,得出∠BFC=90°即可.
試題解析:(1)、∵∠CAB=∠EAD=90°, ∴∠CAE=∠BAD. 在△CAE和△BAD中,
 , ∴△CAE≌△BAD(SAS), ∴CE=BD.
, ∴△CAE≌△BAD(SAS), ∴CE=BD.
(2)、延長BD交CE于F,如圖所示: ∵△CAE≌△BAD, ∴∠ACE=∠ABD, ∵∠CAB=90°,
∴∠ABC+∠ACB=90°, 即∠ABD+∠DBC+∠ACB=90°, ∴∠DBC+∠ACB+∠ACE=90°,
即∠DBC+∠BCF=90°, ∴∠BFC=90°, ∴CE⊥BD.


科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 有兩個角為直角的四邊形是矩形
B. 矩形的對角線相等
C. 平行四邊形的對角線相等
D. 對角線互相垂直的四邊形是菱形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果銷售點用1000元購進甲、乙兩種新出產的水果共140千克,這兩種水果的進價、售價如表所示:
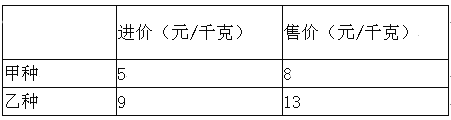
(1)這兩種水果各購進多少千克?
(2)若該水果店按售價銷售完這批水果,獲得的利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,在等邊△ABC中,D是邊AC上一點,連接BD,將△BCD繞點B逆時針旋轉60°,得到△BAE,連接ED,若BC=5,BD=4.則下列結論錯誤的是( ).
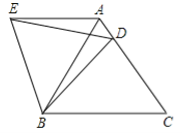
A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等邊三角形 D. △ADE的周長是9
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com