
【題目】甲、乙兩名射擊運動員中進行射擊比賽,兩人在相同條件下各射擊10次,射擊的成績如圖所示.
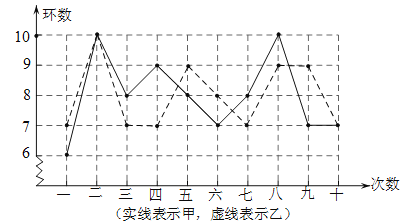
根據圖中信息,回答下列問題:
(1)甲的平均數是___________,乙的中位數是______________;
(2)分別計算甲、乙成績的方差,并從計算結果來分析,你認為哪位運動員的射擊成績更穩定?
【答案】(1)8,7.5 ;(2)乙運動員的射擊成績更穩定.
【解析】試題分析:(1)求甲的平均數只要把甲的十次射擊成績加在一起除以10即可;求乙的中位數先把乙的十次射擊成績按從小到大順序排列,則排在中間兩個數據的平均數就是乙的中位數;(2)先計算出甲,乙的平均數,根據方差計算公式(各個數據與平均數差的平方和再除以10),即可算出兩位運動員的方差,誰的方差小,誰的成績就穩定.
試題解析:(1)把甲的十次射擊成績加在一起除以10:甲的平均數=(6+10+8+9+8+7+8+10+7+7)÷10=8;先把乙的十次射擊成績按從小到大順序排列為7,7,7,7,7,8,9,9,9,10.則排在中間兩個數據是7,8.故乙的中位數是(7+8)÷2=7.5;(2)甲的平均數是8,乙的平均數是(7+7+7+7+7+8+9+9+9+10)÷10=8,故![]()
![]() ,
, ![]() =
=![]() ,
, ![]() ,∴乙運動員的射擊成績更穩定.
,∴乙運動員的射擊成績更穩定.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
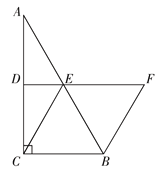
【題目】如圖,在△ABC中,∠ACB=![]() ,D,E分別為AC,AB的中點,BF∥CE交DE的延長線于點F.
,D,E分別為AC,AB的中點,BF∥CE交DE的延長線于點F.
(1)求證:四邊形ECBF是平行四邊形;
(2) 當∠A=![]() 時,求證:四邊形ECBF是菱形.
時,求證:四邊形ECBF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
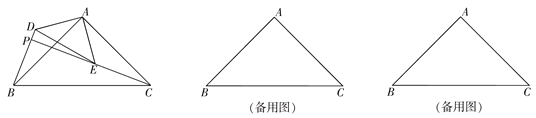
【題目】如圖,△ABC和△ADE是有公共頂點的等腰直角三角形,∠BAC=∠DAE=![]() ,點P為射線BD,CE的交點.
,點P為射線BD,CE的交點.
(1)求證:BD=CE;
(2)若AB=2,AD=1,把△ADE繞點A旋轉,
①當∠EAC=![]() 時,求PB的長;
時,求PB的長;
②直接寫出旋轉過程中線段PB長的最小值與最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com