
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,對稱軸為x=1,給出下列結論:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正確的結論是 . (寫出正確命題的序號) 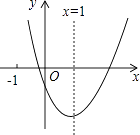
【答案】①④
【解析】解:由二次函數圖象開口向上,得到a>0;與y軸交于負半軸,得到c<0, ∵對稱軸在y軸右側,且﹣ ![]() =1,即2a+b=0,
=1,即2a+b=0,
∴a與b異號,即b<0,
∴abc>0,選項①正確;
∵二次函數圖象與x軸有兩個交點,
∴△=b2﹣4ac>0,即b2>4ac,選項②錯誤;
∵原點O與對稱軸的對應點為(2,0),
∴x=2時,y<0,即4a+2b+c<0,選項③錯誤;
∵x=﹣1時,y>0,
∴a﹣b+c>0,
把b=﹣2a代入得:3a+c>0,選項④正確,
故答案是:①④.
【考點精析】掌握二次函數圖象以及系數a、b、c的關系是解答本題的根本,需要知道二次函數y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關:對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標:(0,c).


科目:初中數學 來源: 題型:
【題目】問題背景:
如圖①,在四邊形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究線段AC,BC,CD之間的數量關系.
小吳同學探究此問題的思路是:將△BCD繞點D,逆時針旋轉90°到△AED處,點B,C分別落在點A,E處(如圖②),易證點C,A,E在同一條直線上,并且△CDE是等腰直角三角形,所以CE= ![]() CD,從而得出結論:AC+BC=
CD,從而得出結論:AC+BC= ![]() CD.
CD.
簡單應用:
(1)在圖①中,若AC= ![]() ,BC=2
,BC=2 ![]() ,則CD= .
,則CD= .
(2)如圖③,AB是⊙O的直徑,點C、D在⊙上, ![]() =
= ![]() ,若AB=13,BC=12,求CD的長.
,若AB=13,BC=12,求CD的長.
拓展規律:
(3)如圖④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的長(用含m,n的代數式表示)
(4)如圖⑤,∠ACB=90°,AC=BC,點P為AB的中點,若點E滿足AE= ![]() AC,CE=CA,點Q為AE的中點,則線段PQ與AC的數量關系是 .
AC,CE=CA,點Q為AE的中點,則線段PQ與AC的數量關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,⊙O為△ABC的外接圓,BC為直徑,點E在AB上,過點E作EF⊥BC,點G在FE的延長線上,且GA=GE. 
(1)求證:AG與⊙O相切.
(2)若AC=6,AB=8,BE=3,求線段OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點O為坐標原點,A,B,C三點的坐標為( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),點D在第一象限,且∠ADB=60°,則線段CD的長的最小值為 .
,0)、(0,5),點D在第一象限,且∠ADB=60°,則線段CD的長的最小值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鮮花銷售部在春節前20天內銷售一批鮮花.其中,該銷售部公司的鮮花批發部日銷售量y1(萬朵)與時間x(x為整數,單位:天)關系為二次函數,部分對應值如表所示.
時間x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
銷量y1(萬朵) | 0 | 16 | 24 | 24 | 16 | 0 |
與此同時,該銷售部還通過某網絡電子商務平臺銷售鮮花,網上銷售日銷售量y2(萬朵)與時間x(x為整數,單位:天) 的函數關系如圖所示.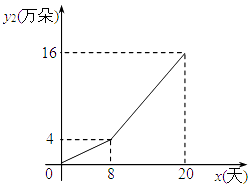
(1)求y1與x的二次函數關系式及自變量x的取值范圍;
(2)求y2與x的函數關系式及自變量x的取值范圍;
(3)當8≤x≤20時,設該花木公司鮮花日銷售總量為y萬朵,寫出y與時間x的函數關系式,并判斷第幾天日銷售總量y最大,并求出此時的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,以BC為半徑作⊙B,交AB于點D,交AB的延長線于點E,連接CD、CE. 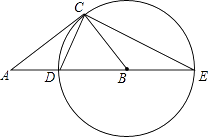
(1)求證:△ACD∽△AEC;
(2)當 ![]() =
= ![]() 時,求tanE;
時,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面積.
,求△ACE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,BC是⊙O的切線,切點為B,OC相交于點D,且CD=2,BC=4, 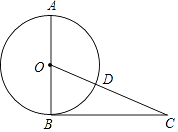
(1)求⊙O的半徑;
(2)連接AD并延長,交BC于點E,取BE的中點F,連接DF,試判斷DF與⊙O的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC、△DCE、△FEG為等邊三角形,邊長分別為2、3、5,且從左至右如圖排列,連接BF,交DC、DE分別于M、N兩點,則△DMN的面積為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CB=CA,∠ACB=90°,點D在邊BC上(與B、C不重合),四邊形ADEF為正方形,過點F作FG⊥CA,交CA的延長線于點G,連接FB,交DE于點Q,給出以下結論: ①AC=FG;②S△FAB:S四邊形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正確的結論的個數是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com