
【題目】如圖![]() ,點(diǎn)
,點(diǎn)![]() 將線段
將線段![]() 分成兩部分,如果
分成兩部分,如果![]() ,那么稱點(diǎn)
,那么稱點(diǎn)![]() 為線段
為線段![]() 的黃金分割點(diǎn),某教學(xué)興趣小組在進(jìn)行研究時,由“黃金分割點(diǎn)”聯(lián)想到“黃金分割線”,類似的給出“黃金分割線”的定義:“一直線將一個面積為
的黃金分割點(diǎn),某教學(xué)興趣小組在進(jìn)行研究時,由“黃金分割點(diǎn)”聯(lián)想到“黃金分割線”,類似的給出“黃金分割線”的定義:“一直線將一個面積為![]() 的圖形分成兩部分,這兩部分的面積分別為
的圖形分成兩部分,這兩部分的面積分別為![]() ,
,![]() ,如果
,如果![]() ,那么稱這條直線為該圖形的黃金分割線.
,那么稱這條直線為該圖形的黃金分割線.
![]() 如圖
如圖![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分線交
的平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,請問直線
,請問直線![]() 是不是
是不是![]() 的黃金分割線,并證明你的結(jié)論;
的黃金分割線,并證明你的結(jié)論;
![]() 如圖
如圖![]() ,在邊長為
,在邊長為![]() 的正方形
的正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 是邊
是邊![]() 上一點(diǎn),若直線
上一點(diǎn),若直線![]() 是正方形
是正方形![]() 的黃金分割線,求
的黃金分割線,求![]() 的長.
的長.
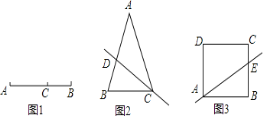
【答案】![]() 直線
直線![]() 是
是![]() 的黃金分割線,理由見解析;(2)
的黃金分割線,理由見解析;(2)![]() 長為
長為![]() .
.
【解析】
(1)如圖2,根據(jù)等高三角形的面積比等于底的比可得![]() ,
,![]() ,
,
要證直線CD是△ABC的黃金分割線,只需證![]() ,只需證
,只需證![]() ,易證BC=AD,只需證
,易證BC=AD,只需證![]() ,只需證△BCD∽△BAC即可;
,只需證△BCD∽△BAC即可;
(2)設(shè)BE=x,如圖3,易得![]() ,
,![]() ,
,![]() .由直線AE是正方形ABCD的黃金分割線可得
.由直線AE是正方形ABCD的黃金分割線可得![]() ,由此得到關(guān)于x的方程,解這個方程就可解決問題.
,由此得到關(guān)于x的方程,解這個方程就可解決問題.
解:![]() 直線
直線![]() 是
是![]() 的黃金分割線.
的黃金分割線.
理由:如圖![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,

∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴直線![]() 是
是![]() 的黃金分割線;
的黃金分割線;
![]() 設(shè)
設(shè)![]() ,如圖
,如圖![]() ,
,
∵正方形![]() 的邊長為
的邊長為![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵直線![]() 是正方形
是正方形![]() 的黃金分割線,
的黃金分割線,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() .
.
∵點(diǎn)![]() 是邊
是邊![]() 上一點(diǎn),
上一點(diǎn),
∴![]() ,
,
∴![]() ,
,
∴![]() 長為
長為![]() .
.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業(yè)安徽少年兒童出版社系列答案
暑假作業(yè)安徽少年兒童出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我國的農(nóng)作物主要以水稻、玉米和小麥為主,種植太單調(diào)不利于土壤環(huán)境的維護(hù),而且對農(nóng)業(yè)的發(fā)展也沒有促進(jìn)作用,為了鼓勵大豆的種植,國家對種植大豆的農(nóng)民給予補(bǔ)貼,調(diào)動農(nóng)民種植大豆的積極性.我市乃大豆之鄉(xiāng),今年很多合作社調(diào)整種植結(jié)構(gòu),把種植玉米改成種植大豆,今年我市某合作社共收獲大豆200噸,計劃采用批發(fā)和零售兩種方式銷售.經(jīng)市場調(diào)查,批發(fā)平均每天售出14噸,由于今年我市小型大豆深加工企業(yè)的增多,預(yù)計能提前完成銷售任務(wù),在平均每天批發(fā)量不變的情況下,實(shí)際平均每天的零售量比原計劃的2倍還多14噸,結(jié)果提前5天完成銷售任務(wù)。那么原計劃零售平均每天售出多少噸?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在等邊三角形ABC中,點(diǎn)P在△ABC內(nèi),點(diǎn)Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求證:△ABP≌△ACQ;
(2)請判斷△APQ是什么三角形,試說明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)y=kx+b的圖象與反比例函數(shù)![]() (x>0)的圖象交于A(2,﹣1),B(
(x>0)的圖象交于A(2,﹣1),B(![]() ,n)兩點(diǎn),直線y=2與y軸交于點(diǎn)C.
,n)兩點(diǎn),直線y=2與y軸交于點(diǎn)C.

(1)求一次函數(shù)與反比例函數(shù)的解析式;
(2)求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 是
是![]() 軸上的兩個定點(diǎn).
軸上的兩個定點(diǎn).
(1)當(dāng)線段![]() 向左平移到某個位置時,若
向左平移到某個位置時,若![]() 的值最小,求平移的距離.
的值最小,求平移的距離.
(2)當(dāng)線段![]() 向左或向右平移時,是否存在某個位置,使四邊形
向左或向右平移時,是否存在某個位置,使四邊形![]() 的周長最小?請說明如何平移?若不存在,請說明理由.
的周長最小?請說明如何平移?若不存在,請說明理由.
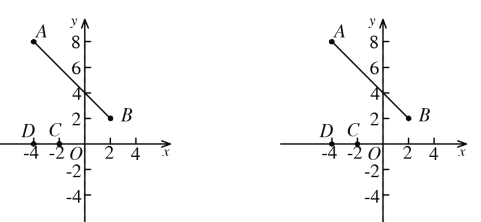
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀理解:對于一些次數(shù)較高或者是比較復(fù)雜的式子進(jìn)行因式分解時,換元法是一種常用的方法,下面是某同學(xué)用換元法對多項(xiàng)式![]() 進(jìn)行因式分解的過程.
進(jìn)行因式分解的過程.
解:設(shè)![]()
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列問題:
(1)該同學(xué)第二步到第三步運(yùn)用了因式分解的__________(填代號).
A.提取公因式 B.平方差公式
C.兩數(shù)和的完全平方公式 D.兩數(shù)差的完全平方公式
(2)按照“因式分解,必須進(jìn)行到每一個多項(xiàng)式因式都不能再分解為止”的要求,該多項(xiàng)式分解因式的最后結(jié)果為______________.
(3)請你模仿以上方法對多項(xiàng)式![]() 進(jìn)行因式分解.
進(jìn)行因式分解.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
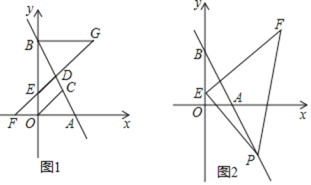
【題目】如圖1,直線![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),
兩點(diǎn),![]() 平分
平分![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 上一點(diǎn),過點(diǎn)
上一點(diǎn),過點(diǎn)![]() 作
作![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,已知
,已知![]() ,
,![]() ,且
,且![]() 滿足
滿足![]() .
.
(1)求![]() 兩點(diǎn)的坐標(biāo);
兩點(diǎn)的坐標(biāo);
(2)若點(diǎn)![]() 為
為![]() 中點(diǎn),延長
中點(diǎn),延長![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,在
,在![]() 的延長線上取點(diǎn)
的延長線上取點(diǎn)![]() ,使
,使![]() ,連接
,連接![]() .
.
①![]() 與
與![]() 軸的位置關(guān)系怎樣?說明理由;
軸的位置關(guān)系怎樣?說明理由;
②求![]() 的長;
的長;
(3)如圖2,若點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() 是
是![]() 軸的正半軸上一動點(diǎn),
軸的正半軸上一動點(diǎn),![]() 是直線
是直線![]() 上一點(diǎn),且
上一點(diǎn),且![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,是否存在點(diǎn)
,是否存在點(diǎn)![]() 使
使![]() 為等腰直角三角形?若存在,求出點(diǎn)
為等腰直角三角形?若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,說明理由.
的坐標(biāo);若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在同一直角坐標(biāo)系中,函數(shù)y=mx+m和函數(shù)y=mx2+2x+2(m是常數(shù),且m≠0)的圖象可能是( )
A. 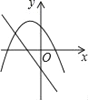 B.
B.  C.
C. 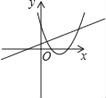 D.
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
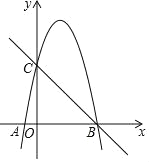
【題目】如圖,拋物線y=﹣x2+4x+5與x軸,y軸分別交于A,B,C三點(diǎn).
(1)請直接寫出A,B,C三點(diǎn)坐標(biāo):A(_____,_____)、B(_____,______)、C(______,______)
(2)若⊙M過A、B、C三點(diǎn),求圓心M的坐標(biāo),并求⊙M的面積;
(3)在(2)的條件下,在拋物線上是否存在點(diǎn)N,使得由A,C,M,N四點(diǎn)構(gòu)成的四邊形為平行四邊形?若存在,請求出點(diǎn)N的坐標(biāo),若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com