
【題目】如圖,在Rt△ABC中,∠ACB=90°,△DCE是△ABC繞著點C順時針方向旋轉得到的,此時B、C、E在同一直線上.
(1)旋轉角的大小;
(2)若AB=10,AC=8,求BE的長.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,三角形ABC中,AC=BC,D是BC上的一點,連接AD,DF平分∠ADC交∠ACB的外角∠ACE的平分線于F.
(1)求證:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家商店準備進行裝修,若請甲、乙兩個裝修隊同時施工,8天完成,需付兩隊共3520元費用;若先請甲隊單獨做6天,再請乙隊單獨做12天可以完成,需付兩隊共3480元費用。
(1)甲、乙兩隊工作一天,商場各應付多少元?
(2)單獨請哪個隊裝修,商場所付費用最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠計劃在規定時間內生產24000個零件.由于銷售商突然急需供貨,工廠實際工作效率比原計劃提高了50%,并提前5天完成這批零件的生產任務.求該工廠原計劃每天加工這種零件多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一元一次方程的根是一元一次不等式組的解,則稱該一元一次方程為該不等式組的相伴方程.
(1)在方程![]() ①,
①,![]() ②,
②,![]() ③中,寫出是不等式組
③中,寫出是不等式組![]() 的相伴方程的序號 .
的相伴方程的序號 .
(2)寫出不等式組![]() 的一個相伴方程,使得它的根是整數: .
的一個相伴方程,使得它的根是整數: .
(3)若方程![]() 都是關于
都是關于![]() 的不等式組
的不等式組![]() 的相伴方程,求
的相伴方程,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究題:已知:如圖,![]() ,
,![]() .求證:
.求證:![]() .
.
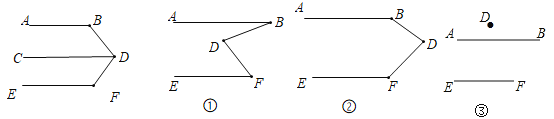
老師要求學生在完成這道教材上的題目證明后,嘗試對圖形進行變形,繼續做拓展探究,看看有什么新發現?
(1)小穎首先完成了對這道題的證明,在證明過程中她用到了平行線的一條性質,小穎用到的平行線性質可能是 .
(2)接下來,小穎用《幾何畫板》對圖形進行了變式,她先畫了兩條平行線![]() ,然后在平行線間畫了一點
,然后在平行線間畫了一點![]() ,連接
,連接![]() 后,用鼠標拖動點
后,用鼠標拖動點![]() ,分別得到了圖
,分別得到了圖![]()
![]() ,小穎發現圖
,小穎發現圖![]() 正是上面題目的原型,于是她由上題的結論猜想到圖
正是上面題目的原型,于是她由上題的結論猜想到圖![]() 和
和![]() 圖中的與
圖中的與![]() 之間也可能存在著某種數量關系.于是她利用《幾何畫板》的度量與計算功能,找到了這三個角之間的數量關系.
之間也可能存在著某種數量關系.于是她利用《幾何畫板》的度量與計算功能,找到了這三個角之間的數量關系.
請你在小穎操作探究的基礎上,繼續完成下面的問題:
(ⅰ)猜想圖![]() 中
中![]() 與
與![]() 之間的數量關系并加以證明;
之間的數量關系并加以證明;
(ⅱ)補全圖![]() ,直接寫出
,直接寫出![]() 與
與![]() 之間的數量關系: .
之間的數量關系: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列四個關于是否成反比例的命題,判斷它們的真假.
(1)面積一定的等腰三角形的底邊長和底邊上的高成反比例;
(2)面積一定的菱形的兩條對角線長成反比例;
(3)面積一定的矩形的兩條對角線長成反比例;
(4)面積一定的直角三角形的兩直角邊長成比例.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com