
【題目】我們知道,任意一個正整數![]() 都可以進行這樣的分解:
都可以進行這樣的分解: ![]() (
(![]() ,
, ![]() 是正整數,且
是正整數,且![]() ),在
),在![]() 的所有這種分解中,如果
的所有這種分解中,如果![]() ,
, ![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是
是![]() 的最佳分解,并規定:
的最佳分解,并規定: ![]() .
.
例如![]() 可以分解成
可以分解成![]() ,
, ![]() 或
或![]() ,因為
,因為![]() ,所以
,所以![]() 是
是![]() 的最佳分解,所以
的最佳分解,所以![]() .
.
(![]() )求出
)求出![]() 的值.
的值.
(![]() )如果一個兩位正整數
)如果一個兩位正整數![]() ,
, ![]() (
(![]() ,
, ![]() ,
, ![]() 為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為
為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為![]() ,那么我們稱這個數
,那么我們稱這個數![]() 為“文瀾數”,求所有“文瀾數”并寫出所有“文瀾數”中
為“文瀾數”,求所有“文瀾數”并寫出所有“文瀾數”中![]() 的最小值.
的最小值.
科目:初中數學 來源: 題型:
【題目】探究題.
用棋子擺成的“T”字形圖如圖所示:

(1)填寫表:
圖形序號 | ① | ② | ③ | ④ | … | ⑩ |
每個圖案中棋子個數 | 5 | 8 | … |
(2)寫出第n個“T”字形圖案中棋子的個數(用含n的代數式表示);
(3)第20個“T”字形圖案共有棋子多少個?
(4)計算前20個“T”字形圖案中棋子的總個數.(提示:請你先思考下列問題:第1個圖案與第20個圖案中共有多少個棋子?第2個圖案與第19個圖案中共有多少個棋子?第3個圖案與第18個圖案呢?)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某數學興趣小組為了測量河對岸l1的兩棵古樹A、B之間的距離,他們在河這邊沿著與AB平行的直線l2上取C、D兩點,測得∠ACB=15°,∠ACD=45°,若l1、l2之間的距離為50m,則古樹A、B之間的距離為m. 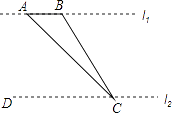
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰直角三角形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是斜邊
是斜邊![]() 的中點,連接
的中點,連接![]() .
.
(1)如圖1, ![]() 是
是![]() 的中點,連接
的中點,連接![]() ,將
,將![]() 沿
沿![]() 翻折到
翻折到![]() ,連接
,連接![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
(2)如圖2,在![]() 上取一點
上取一點![]() ,使得
,使得![]() ,連接
,連接![]() ,將
,將![]() 沿
沿![]() 翻折到
翻折到![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,求證:
,求證: ![]() .
.
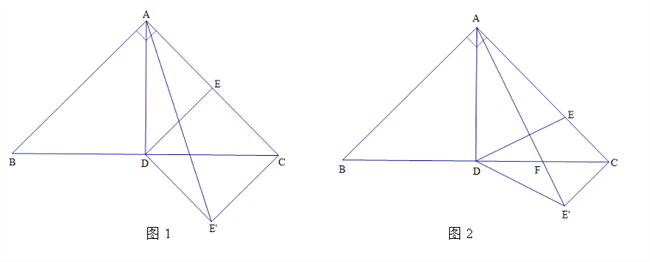
查看答案和解析>>
科目:初中數學 來源: 題型:
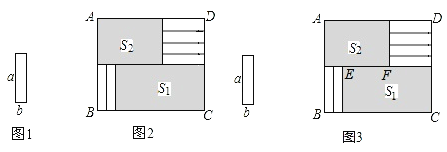
【題目】將6張小長方形紙片(如圖1所示)按圖2所示的方式不重疊的放在長方形ABCD內,未被覆蓋的部分恰好分割為兩個長方形,面積分別為S1和S2.已知小長方形紙片的長為a,寬為b,且a>b.當AB長度不變而BC變長時,將6張小長方形紙片還按照同樣的方式放在新的長方形ABCD內,S1與S2的差總保持不變,求a,b滿足的關系式.
(1)為解決上述問題,如圖3,小明設EF=x,則可以表示出S1=_________,S2=_________;
(2)求a,b滿足的關系式,寫出推導過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c的頂點為Q,拋物線與x軸交于A(﹣1,0),B(5,0)兩點,與y軸交于點C.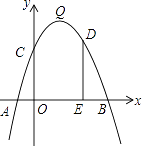
(1)求拋物線的解析式及其頂點Q的坐標;
(2)在該拋物線上求一點P,使得S△PAB=S△ABC , 求出點P的坐標:
(3)若點D是第一象限拋物線上的一個動點,過點D作DE⊥x軸,垂足為E.有一個同學說:“在第一象限拋物線上的所有點中,拋物線的頂點Q與x軸相距最遠,所以當點D運動至點Q時,折線D﹣E﹣O的長度最長.”這個同學的說法正確嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com