
【題目】如圖,已知△DEF中,DE=17cm,EF=30cm,EF邊上的中線DG=8cm.
求證:△DEF是等腰三角形.
【答案】解:∵DG是EF邊上的中線,EF=30cm,
∴EG=15cm,
∵DE=17cm,DG=8cm,
∴EG2+DG2=DE2 ,
∴DG⊥EF,
∴△DGE≌△DGF,
∴DE=DF,
∴△DEF是等腰三角形.
【解析】根據已知條件利用勾股定理求得DG⊥EF,又知EG=GF,可證明△DGE≌△DGF,所以可推出△DEF是等腰三角形.
【考點精析】關于本題考查的等腰三角形的判定和勾股定理的概念,需要了解如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(簡稱:等角對等邊).這個判定定理常用于證明同一個三角形中的邊相等;直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2才能得出正確答案.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
【題目】小亮房間窗戶的窗簾如圖1所示,它是由兩個四分之一圓組成(半徑相同) 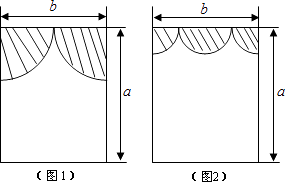
(1)用代數式表示窗戶能射進陽光的面積是 ab﹣ ![]() πb2 . (結果保留π)
πb2 . (結果保留π)
(2)當 ![]() ,b=1時,求窗戶能射進陽光的面積是多少?(取π≈3)
,b=1時,求窗戶能射進陽光的面積是多少?(取π≈3)
(3)小亮又設計了如圖2的窗簾(由一個半圓和兩個四分之一圓組成,半徑相同),請你幫他算一算此時窗戶能射進陽光的面積是否更大?如果更大,那么大多少?(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】收集和整理數據.
某中學七(1)班學習了統計知識后,數學老師要求每個學生就本班學生的上學方式進行一次全面調查,如圖是一同學通過收集數據后繪制的兩幅不完整的統計圖,請根據圖中提供的信息,解答下列問題:(每個學生只選擇1種上學方式).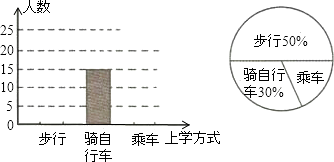
(1)求該班乘車上學的人數;
(2)將頻數分布直方圖補充完整;
(3)若該校七年級有1200名學生,能否由此估計出該校七年級學生騎自行車上學的人數,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學庫存960套舊課桌椅準備修理。現有甲、乙兩個木工小組都想承接這項業務。經協商后得知:甲小組單獨修理這批桌椅比乙小組多用20天;乙小組每天比甲小組多修8套;學校每天需付甲小組修理費80元,付乙小組120元。
(1)求甲、乙兩個小組每天各修理桌櫈多少套?
(2)在修理過程中,學校要委派一名修理工進行質量監督,并由學校負擔他每天的生活補助10元,現有以下三種修理方案供選擇:①由甲單獨修理;②由乙單獨修理;③由甲、乙共同合作修理。你認為哪種方案既省時又省錢?試比較說明。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com