
【題目】如圖是按規律擺放在墻角的一些小正方體,從上往下分別記為第一層,第二層,第三層,…,第n層.
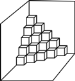
(1)第三層有________個小正方體;
(2)從第四層至第六層(含第四層和第六層)共有________個小正方體;
(3)第n層有________個小正方體;
(4)若每個小正方體邊長為a分米,共擺放了n層,則要將擺放的小正方體能看到的表面部分涂上防銹漆,則防銹漆的總面積為________平方分米.
【答案】(1)6(2)46(3)![]() (4)
(4)![]() a2n(n+1)
a2n(n+1)
【解析】
(1)第1個圖有1層,共1個小正方體,第2個圖有2層,第2層正方體的個數為1+2,以此類推第三層即可;
(2)第4至6層求出每層個數相加即可;
(3)根據相應規律可得第n層正方體的個數為1+2+3+…+n=![]() ;
;
(4)共擺放n層,根據正面、右面、上面小正方形的面的個數,求出總面數再乘每一個小正方形的面積即可.
解:(1)第1層,共1個小正方體,
第2層正方體的個數為1+2=3,
第3層正方體的個數為:1+2+3=6.
故答案為:6.
(2)第4層正方體的個數為:10,
第5層正方體的個數為:15,
第6層正方體的個數為:21,
所以從第四層至第六層(含第四層和第六層)共有:10+15+21=46.
故答案為:46.
(3)根據(1)相應規律,可得第n層正方體的個數為1+2+3+…+n=![]() ;
;
(4)共擺放n層,則正面小正方形的面的個數:2×(1+2+3+…+n)=n(n+1),
右面小正方形的面的個數:1+2+3+…+n=![]() ,
,
所以涂上防銹漆的面積為:[n(n+1)+![]() ]×a2=
]×a2=![]() a2n(n+1)分米2.
a2n(n+1)分米2.
故答案為:(1)6;(2)41;(3)![]() ;(4)
;(4)![]() a2n(n+1).
a2n(n+1).


科目:初中數學 來源: 題型:
【題目】6月5日是世界環境日,為了普及環保知識,增強環保意識,某市第一中學舉行了“環保知識競賽”,參賽人數為1 000人.為了了解本次競賽的成績情況,學校團委從中抽取部分學生的成績(滿分為100分,最少為50分,得分取整數)進行統計,并繪制出不完整的頻數分布表和不完整的頻數分布直方圖如下:
分組 | 頻數 | 所占百分比 |
49.5~59.5 | 8 | 8% |
59.5~69.5 | __ __ | 12% |
69.5~79.5 | 20 | __ __ |
79.5~89.5 | 32 | __ __ |
89.5~100.5 | __ __ | 28% |
(1)補全頻數分布表和頻數分布直方圖;
(2)若成績在80分以上為優秀,求這次參賽的學生中成績為優秀的約有多少人.
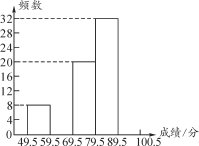
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校隨機抽取部分學生,就”對自己做錯題進行整理、分析、改正”這一學習習慣進行問卷調查,選項為:很少、有時、常常、總是![]() 每人只能選一項
每人只能選一項![]() ;調查數據進行了整理,繪制成部分統計圖如圖:
;調查數據進行了整理,繪制成部分統計圖如圖:
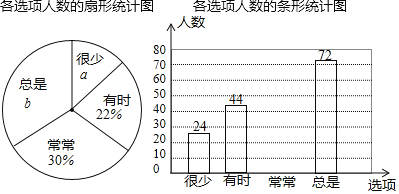
請根據圖中信息,解答下列問題:
![]() 該調查的總人數為______,
該調查的總人數為______,![]() ______
______![]() ,
,![]() ______
______![]() ,“常常”對應扇形的圓心角的度數為______;
,“常常”對應扇形的圓心角的度數為______;
![]() 請你補全條形統計圖;
請你補全條形統計圖;
![]() 若該校有2000名學生,請你估計其中”總是”對錯題進行整理、分析、改正的學生有多少名?
若該校有2000名學生,請你估計其中”總是”對錯題進行整理、分析、改正的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD是菱形,E是BD延長線上一點,F是DB延長線上一點,且DE=BF.請你以F為一個端點,和圖中已標明字母的某一點連成一條新的線段,猜想并證明它和圖中已有的某一條線段相等(只須證明一組線段相等即可).
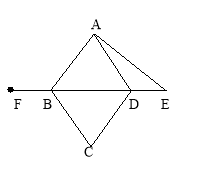
(1)連接 ;
(2)猜想: = ;
(3)證明:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察一組數據:2,4,7,11,16,22,29,…,它們有一定的規律,若記第一個數為a1,第二個數記為a2,…,第n個數記為an.
(1)請寫出29后面的第一個數;
(2)通過計算a2-a1,a3-a2,a4-a3,…由此推算a100-a99的值;
(3)根據你發現的規律求a100的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點G,D,C在直線a上,點E,F,A,B在直線b上,若a∥b,Rt△GEF從如圖所示的位置出發,沿直線b向右勻速運動,直到EG與BC重合.運動過程中△GEF與矩形ABCD重合部分的面積(S)隨時間(t)變化的圖象大致是( )

A.  B.
B.  C.
C. 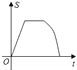 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個整數能表示成a2+b2(a、b是正整數)的形式,則稱這個數為“豐利數”.例如,2是“豐利數”,因為2=12+12,再如,M=x2+2xy+2y2=(x+y)2+y2(x+y,y是正整數),所以M也是“豐利數”.
(1)請你寫一個最小的三位“豐利數”是 ,并判斷20 “豐利數”.(填是或不是);
(2)已知S=x2+y2+2x﹣6y+k(x、y是整數,k是常數),要使S為“豐利數”,試求出符合條件的一個k值(10≤k<200),并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com