
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在
在![]() 上,且
上,且![]() 的半徑為
的半徑為![]() .問當(dāng)
.問當(dāng)![]() 在什么范圍內(nèi)取值時
在什么范圍內(nèi)取值時![]() 與
與![]() 相離、相切、相交?
相離、相切、相交?

【答案】當(dāng)![]() 時,
時,![]() 與
與![]() 相離;
相離;![]() 時,
時,![]() 與
與![]() 相切;
相切;![]() 時,
時,![]() 與
與![]() 相交.
相交.
【解析】
由三角形的內(nèi)角和可求出∠A的大小,根據(jù)含30°直角三角形的性質(zhì)即可得到OD和AO的關(guān)系,
(1)若圓O與AC相離,則有OD大于r,列出關(guān)于x的不等式,求出不等式的解集即可得到x的范圍;
(2)若圓O與AC相切,則有OD=r,求出x的值即可;
(3)若圓O與AC相交,則有OD小于r,列出關(guān)于x的不等式,求出不等式的解集即可得到x的范圍.
作![]() ,如圖所示:
,如圖所示:
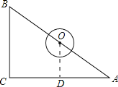
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() 若圓
若圓![]() 與
與![]() 相離,則有
相離,則有![]() 大于
大于![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
![]() 若圓
若圓![]() 與
與![]() 相切,則有
相切,則有![]() 等于
等于![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
![]() 若圓
若圓![]() 與
與![]() 相交,則有
相交,則有![]() 小于
小于![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
綜上可知:當(dāng)![]() 時,
時,![]() 與
與![]() 相離;
相離;![]() 時,
時,![]() 與
與![]() 相切;
相切;![]() 時,
時,![]() 與
與![]() 相交.
相交.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀理解:
為解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我們可以將x2﹣1視為一個整體,然后設(shè)x2﹣1=y,則原方程化為y2﹣5y+4=0,解此方程得:y1=1,y2=4.
當(dāng)y=1時,x2﹣1═1,∴x=±![]() .
.
當(dāng)y=4時,x2﹣1═4,∴x=±![]() .
.
∴原方程的解為:x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]() .
.
以上方法叫做換元法解方程,達(dá)到了降次的目的,體現(xiàn)了轉(zhuǎn)化思想.
運(yùn)用上述方法解方程:x4﹣8x2+12=0.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,以點(diǎn)P(-1,0)為圓心的圓,交x軸于B、C兩點(diǎn)(B在C的左側(cè)),交y軸于A、D兩點(diǎn)(A在D的下方),AD=![]() ,將△ABC繞點(diǎn)P旋轉(zhuǎn)180°,得到△MCB.
,將△ABC繞點(diǎn)P旋轉(zhuǎn)180°,得到△MCB.

(1)求B、C兩點(diǎn)的坐標(biāo);
(2)請在圖中畫出線段MB、MC,并判斷四邊形ACMB的形狀(不必證明),求出點(diǎn)M的坐標(biāo);
(3)動直線l從與BM重合的位置開始繞點(diǎn)B順時針旋轉(zhuǎn),到與BC重合時停止,設(shè)直線l與CM交點(diǎn)為E,點(diǎn)Q為BE的中點(diǎn),過點(diǎn)E作EG⊥BC于G,連接MQ、QG.請問在旋轉(zhuǎn)過程中∠MQG的大小是否變化?若不變,求出∠MQG的度數(shù);若變化,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,點(diǎn)
厘米,點(diǎn)![]() 為
為![]() 的中點(diǎn).如果點(diǎn)
的中點(diǎn).如果點(diǎn)![]() 在線段
在線段![]() 上以每秒2厘米的速度由
上以每秒2厘米的速度由![]() 點(diǎn)向
點(diǎn)向![]() 點(diǎn)運(yùn)動,同時,點(diǎn)
點(diǎn)運(yùn)動,同時,點(diǎn)![]() 在線段
在線段![]() 上以每秒
上以每秒![]() 厘米的速度由
厘米的速度由![]() 點(diǎn)向
點(diǎn)向![]() 點(diǎn)運(yùn)動,設(shè)運(yùn)動時間為
點(diǎn)運(yùn)動,設(shè)運(yùn)動時間為![]() (秒)
(秒)![]() .
.

(1)用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() 的長度;
的長度;
(2)若點(diǎn)![]() 、
、![]() 的運(yùn)動速度相等,經(jīng)過1秒后,
的運(yùn)動速度相等,經(jīng)過1秒后,![]() 與
與![]() 是否全等,請說明理由;
是否全等,請說明理由;
(3)若點(diǎn)![]() 、
、![]() 的運(yùn)動速度不相等,當(dāng)點(diǎn)
的運(yùn)動速度不相等,當(dāng)點(diǎn)![]() 的運(yùn)動速度
的運(yùn)動速度![]() 為多少時,能夠使
為多少時,能夠使![]() 與
與![]() 全等?
全等?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,高速公路上有A、B兩點(diǎn)相距25km,C、D為兩村莊,已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,現(xiàn)要在AB上建一個服務(wù)站E,使得C、D兩村莊到E站的距離相等,則AE的長是( )km.

A.5B.10C.15D.25
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖(1),Rt△ABC中,∠ACB=-90°,CD⊥AB,垂足為D.AF平分∠CAB,交CD于點(diǎn)E,交CB于點(diǎn)F
(1)求證:CE=CF.
(2)將圖(1)中的△ADE沿AB向右平移到△A’D’E’的位置,使點(diǎn)E’落在BC邊上,其它條件不變,如圖(2)所示.試猜想:BE'與CF有怎樣的數(shù)量關(guān)系?請證明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,AB=AC,AD是△ABC的角平分線,點(diǎn)O為AB的中點(diǎn),連接DO并延長到點(diǎn)E,使OE=OD,連接AE,BE.

(1)求證:四邊形AEBD是矩形;
(2)當(dāng)△ABC滿足什么條件時,矩形AEBD是正方形,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
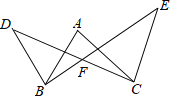
【題目】如圖,AB=BD,AC=CE,DC、BE交于點(diǎn)F,∠ABD=∠ACE=60°.
(1)求證:BE=CD;
(2)求∠A+∠ABF+∠ACF的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com