
設![]() 是任意兩個不等實數,我們規(guī)定:滿足不等式
是任意兩個不等實數,我們規(guī)定:滿足不等式![]() 的實數
的實數![]() 的所有取值的全體叫做閉區(qū)間,表示為
的所有取值的全體叫做閉區(qū)間,表示為![]() .對于一個函數,如果它的自變量
.對于一個函數,如果它的自變量![]() 與函數值
與函數值![]() 滿足:當
滿足:當![]() 時,有
時,有![]() ,我們就
,我們就![]() 稱此函數是閉區(qū)間
稱此函數是閉區(qū)間![]() 上的“閉函數”.
上的“閉函數”.
(1)反比例函數![]() 是閉區(qū)間
是閉區(qū)間![]() 上的“閉函數”嗎?請判斷并說明理由;
上的“閉函數”嗎?請判斷并說明理由;
(2)若一次函數![]() 是閉區(qū)間
是閉區(qū)間![]() 上的“閉函數”,求此函數的解析式;
上的“閉函數”,求此函數的解析式;
(3)若二次函數![]() 是閉區(qū)間
是閉區(qū)間![]() 上的“閉函數”,求實數
上的“閉函數”,求實數![]() 的值.
的值.
解:(1)是;
由函數![]() 的圖象可知,當
的圖象可知,當![]() 時,函數值
時,函數值![]() 隨著自變量
隨著自變量![]() 的增大而減少,而當
的增大而減少,而當![]() 時,
時,![]() ;
;![]() 時,
時,![]() ,故也有
,故也有![]() ,
,
所以,函數![]() 是閉區(qū)間
是閉區(qū)間![]() 上的“閉函數”.
上的“閉函數”.
(2)因為一次函數![]() 是閉區(qū)間
是閉區(qū)間![]() 上的“閉函數”,所以根據一次函數的圖象與性質,必有:
上的“閉函數”,所以根據一次函數的圖象與性質,必有:
①當![]() 時,
時,![]()
![]() ,解之得
,解之得![]() ,
,![]()
![]()
![]() ,
,
②當![]() 時,
時,![]()
![]() ,解之得
,解之得![]() ,
,![]()
![]()
![]() ,
,
故一次函數的解析式為![]() 或
或![]() .
.
(3)由于函數![]() 的圖象開口向上,且對稱軸為
的圖象開口向上,且對稱軸為![]() ,
,![]()
頂點為![]() ,由題意根據圖象,分以下三種情況討論:
,由題意根據圖象,分以下三種情況討論:
①當![]() 時,必有
時,必有![]() 時,
時,![]() 且
且![]() 時,
時,![]() ,
,
即方程![]() 必有兩個不等實數根,解得
必有兩個不等實數根,解得![]() ,
,
而![]() 分布在2的兩邊,這
分布在2的兩邊,這![]() 與
與![]() 矛盾,舍去;
矛盾,舍去;
②當![]() 時,必有
時,必有![]() 時
時![]() ,
,![]() 且
且 ![]() 時,
時,![]() ,
,
即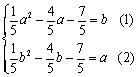
(1)-(2)得![]() 代入(1)得
代入(1)得![]() 或
或 ![]() (舍去),
(舍去),
故此時有![]() 滿足題意;
滿足題意;
③ 當![]() 時,必有函數值
時,必有函數值![]() 的最小值為
的最小值為![]() ,
,
由于此二次函數是閉區(qū)間![]() 上的“閉函數”,故必有
上的“閉函數”,故必有![]() ,
,
從而有![]() ,而當
,而當![]() 時,
時,![]() ,即得點
,即得點![]() ;
;
又點![]() 關于對稱軸
關于對稱軸![]() 的對稱點為
的對稱點為![]() ,
,
由“閉函數”的定義可知必有![]() ,
,![]() , 又由①知
, 又由①知![]()
故可得![]() ,
,![]() 符合題意.
符合題意.
綜上所述,![]() ,
,![]() 或
或![]() ,
,![]() 為所求的實數.
為所求的實數.


科目:初中數學 來源: 題型:
| 2013 |
| x |
| 1 |
| 5 |
| 4 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
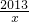 是閉區(qū)間[1,2013]上的“閉函數”嗎?請判斷并說明理由;
是閉區(qū)間[1,2013]上的“閉函數”嗎?請判斷并說明理由; x2-
x2- x-
x- 是閉區(qū)間[a,b]上的“閉函數”,求實數a,b的值.
是閉區(qū)間[a,b]上的“閉函數”,求實數a,b的值.查看答案和解析>>
科目:初中數學 來源:長沙 題型:解答題
| 2013 |
| x |
| 1 |
| 5 |
| 4 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:初中數學 來源:2013年湖南省長沙市中考數學試卷(解析版) 題型:解答題
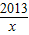 是閉區(qū)間[1,2013]上的“閉函數”嗎?請判斷并說明理由;
是閉區(qū)間[1,2013]上的“閉函數”嗎?請判斷并說明理由; x2-
x2- x-
x- 是閉區(qū)間[a,b]上的“閉函數”,求實數a,b的值.
是閉區(qū)間[a,b]上的“閉函數”,求實數a,b的值.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com