Question

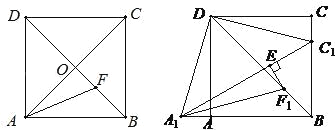
【題目】如圖，在正方形ABCD中，對角線AC與BD相交于點O，AF平分∠BAC，交BD于點F．

（1）求證：；

（2）點A1、點C1分別同時從A、C兩點出發，以相同的速度運動相同的時間后同時停止，如圖，A1F1平分∠BA1C1，交BD于點F1，過點F1作F1E⊥A1C1，垂足為E，請猜想EF1，AB與三者之間的數量關系，并證明你的猜想；

（3）在（2）的條件下，當A1E＝6，C1E＝4時，則BD的長為　　．

Answer 1

【答案】（1）見解析； （2）AB－EF1＝ A1C1 ，理由見解析；（3）

【解析】試題分析：

（1）如下圖，過點F作FG⊥AB于點G，則由AF平分∠CAB和四邊形ABCD是正方形易證△AOF≌△AGF，△BGF是等腰直角三角形，由此可得AO=AG，FG=BG=OF，從而可得AB=AG+BG=AO+OF=AC+OF，變形即可得到結論；

（2）如下圖，過F1作F1G1⊥A1B，過F1作F1H1⊥BC1由此可得四邊形F1G1BH1是矩形．

由已知條件易得EF1＝G1F1＝F1H1，從而可得F1是三角形A1BC1的內心，由“直角三角形內切圓的半徑與三條邊長間的關系”結合CC1=AA1，即可求得EF1，AB與三者之間的數量關系；

（3）如圖，設CC1=AA1=x，由點F1是△A1BC1的內心，點E1、G1、H1都是切點可得A1E＝（A1C1＋A1B－BC1）÷2，即A1E＝[A1C1＋（AB＋x）－（AB－x）]÷2＝（10＋2x）÷2＝6，

由此解得x＝1；然后在Rt△A1BC1中，由A1B2＋BC12＝AC12，可得：（AB＋1）2＋（AB－1）2＝100，解得AB的長即可由BD=AB求得BD的長.

試題解析：

（1）過F作FG⊥AB于G，

∵AF平分∠CAB，FO⊥AC，FG⊥AB，

∴OF＝FG，

∵∠AOF＝∠AGF＝90°，AF＝AF，OF＝FG，

∴△AOF≌△AGF，

∴AO＝AG，

直角三角形BGF中，∠DGA＝45°，

∴FG＝BG＝OF，

∴AB＝AG＋BG＝AO＋OF＝AC＋OF，

∴AB－OF＝AC．

（2）過F1作F1G1⊥A1B，過F1作F1H1⊥BC1，則四邊形F1G1BH1是矩形．

∵BD平分∠ABC，A1F1平分∠BA1C1，

∴F1H1＝F1G1=EF1，

即：F1是三角形A1BC1的內心，

∴EF1＝（A1B＋BC1－A1C1）÷2…①

∵A1B＋BC1＝AB＋A1A＋BC－CC1，而CC1＝A1A，

∴A1B＋BC1＝2AB，

因此①式可寫成：EF1＝（2AB－A1C1）÷2，

即AB－EF1＝A1C1．

（3）由（2）得，F1是三角形A1BC1的內心，且E1、G1、H1都是切點．

∴A1E＝（A1C1＋A1B－BC1）÷2，

如果設CC1＝A1A＝x，

A1E＝[A1C1＋（AB＋x）－（AB－x）]÷2＝（10＋2x）÷2＝6，

∴x＝1，

在直角三角形A1BC1中，根據勾股定理有A1B2＋BC12＝AC12，

即：（AB＋1）2＋（AB－1）2＝100，

解得AB＝7，

∴BD＝7．