
【題目】如圖,⊙O是△ABC的外接圓,AB是⊙O的直徑,D為⊙O上一點,OD⊥AC,垂足為E,連接BD 
(1)求證:BD平分∠ABC;
(2)當∠ODB=30°時,求證:BC=OD.
【答案】
(1)證明:∵OD⊥AC OD為半徑,
∴ ![]() =
= ![]() ,
,
∴∠CBD=∠ABD,
∴BD平分∠ABC
(2)證明:∵OB=OD,
∴∠OBD=∠0DB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB為⊙O的直徑,
∴∠ACB=90°,
在Rt△ACB中,BC= ![]() AB,
AB,
∵OD= ![]() AB,
AB,
∴BC=OD
【解析】(1)由OD⊥AC OD為半徑,根據垂徑定理,即可得 ![]() =
= ![]() ,又由在同圓或等圓中,同弧或等弧所對的圓周角相等,即可證得BD平分∠ABC;(2)首先由OB=OD,易求得∠AOD的度數,又由OD⊥AC于E,可求得∠A的度數,然后由AB是⊙O的直徑,根據圓周角定理,可得∠ACB=90°,繼而可證得BC=OD.
,又由在同圓或等圓中,同弧或等弧所對的圓周角相等,即可證得BD平分∠ABC;(2)首先由OB=OD,易求得∠AOD的度數,又由OD⊥AC于E,可求得∠A的度數,然后由AB是⊙O的直徑,根據圓周角定理,可得∠ACB=90°,繼而可證得BC=OD.
【考點精析】本題主要考查了含30度角的直角三角形和垂徑定理的相關知識點,需要掌握在直角三角形中,如果一個銳角等于30°,那么它所對的直角邊等于斜邊的一半;垂徑定理:平分弦(不是直徑)的直徑垂直于弦,并且平分弦所對的兩條弧才能正確解答此題.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:初中數學 來源: 題型:
【題目】如果把存入3萬元記作+3萬元,那么支出2萬元應記作__________, -4萬元表示的意思是________________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,BC=AC,∠BCA=90°,P為直線AC上一點,過點A作AD⊥BP于點D,交直線BC于點Q.
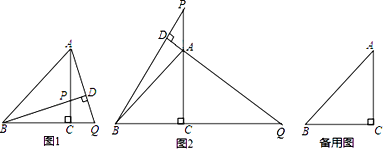
(1)如圖1,當P在線段AC上時,求證:BP=AQ;
(2)如圖2,當P在線段CA的延長線上時,(1)中的結論是否成立?________(填“成立”或“不成立”)
(3)在(2)的條件下,當∠DBA=________時,存在AQ=2BD,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,已知
,已知![]() ,點
,點![]() ,
, ![]() 分別是射線
分別是射線![]() ,
, ![]() 上兩定點,且
上兩定點,且![]() ,
, ![]() ;動點
;動點![]() 從點
從點![]() 向點
向點![]() 運動,以
運動,以![]() 為斜邊向右側作等腰直角
為斜邊向右側作等腰直角![]() .設線段
.設線段![]() 的長
的長![]() ,點
,點![]() 到射線
到射線![]() 的距離為
的距離為![]() .
.
(1)若![]() ,直接寫出點
,直接寫出點![]() 到射線
到射線![]() 的距離;
的距離;
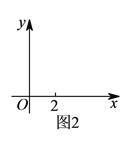
(2)求![]() 關于
關于![]() 的函數表達式,并在圖
的函數表達式,并在圖![]() 中畫出函數圖象;
中畫出函數圖象;
(3)當動點![]() 從點
從點![]() 運動到點
運動到點![]() ,求點
,求點![]() 運動經過的路徑長.
運動經過的路徑長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品的進價為每件50元,售價為每件60元,每個月可賣出200件;如果每件商品的售價每上漲1元,則每個月少賣10件.設每件商品的售價上漲x元(x為正整數),每個月的銷售利潤為y元.
(1)求y與x的函數關系式;
(2)每件商品的售價定為多少元時,每個月可獲得最大利潤?最大的月利潤是多少元?
(3)若每個月的利潤不低于2160元,售價應在什么范圍?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的暗礁區,兩燈塔A,B之間的距離恰好等于圓的半徑,為了使航船(S)不進入暗礁區,那么S對兩燈塔A,B的視角∠ASB必須( ) 
A.大于60°
B.小于60°
C.大于30°
D.小于30°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把矩形紙片ABCD沿EF翻折,點A恰好落在BC邊的A′處,若AB= ![]() ,∠EFA=60°,則四邊形A′B′EF的周長是( )
,∠EFA=60°,則四邊形A′B′EF的周長是( ) 
A.1+3 ![]()
B.3+ ![]()
C.4+ ![]()
D.5+ ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com