Question

【題目】如圖，在菱形中，，為對角線延長線上一點，連接和，為上一點，且滿足，連接，交于點．

（1）若，且，求的長；

（2）證明：．

Answer 1

【答案】（1）；（2）證明過程見詳解

【解析】

（1）首先根據菱形以及等邊三角形的性質，求得∠MAB=90，再證明△BMA△BMC，可得∠BCE=90，再利用勾股定理即可求解；

（2）如圖，在BD上取一點G，使得BG=DF，連接CG交BE于O，只要證明，MG=MC，通過等量代換，即可證明結論．

（1）如圖：

∵四邊形ABCD是菱形，∠BAD=60，

∴△ABD、△BCD都是等邊三角形，

∴∠ABD=∠CBD=∠ADB=∠BAD=60，BA=BC，

∵∠AMB=30，∠ADB=∠AMB+∠DAM，

∴∠DAM=∠DMA=30，

∴∠MAB=90，DA=DM=AB=BC=CE=3，

在△BMA和△BMC中， ，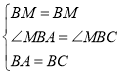

∴△BMA△BMC（SAS），

∴∠BCM=∠BAM=90，

在Rt△BCE中：．

（2）證明：如圖，在BD上取一點G，使得BG=DF，連接CG交BE于O，

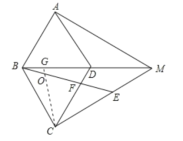
∵BG=DF， ∠CBG=∠BDF，BD=BC，

∴△GBC△FDB，

∴∠GBC=∠BFD，∠DBF=∠BCG，

∴∠MGC=∠BFC，

∵∠COF=∠CBO+∠OCB=∠CBO+∠DBF=60，

在△COE中，∠ECO+∠EOC+∠CEO=180，

在△BCF中，∠BFC+∠CBF+∠BCF=180，

∵CB=CE，

∴∠CBE=∠CEO，

∵∠BCF=∠COE=60，

∴∠ECO=∠BFC=∠MGC，

∴MC=MG，

由（1）知△BMA△BMC，

∴AM=MC=MG，

∵MG=DG+DM， BD=CD，BG=DF，

∴DG=CF，

∴AM=CF+DM．