
【題目】如圖拋物線y=ax2+bx+c的圖象交x軸于A(﹣2,0)和點B,交y軸負半軸于點C,且OB=OC,下列結論:
①2b﹣c=2;②a= ![]() ;③ac=b﹣1;④
;③ac=b﹣1;④ ![]() >0
>0
其中正確的個數有( )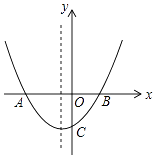
A.1個
B.2個
C.3個
D.4個
【答案】C
【解析】解:據圖象可知a>0,c<0,b>0,
∴ ![]() <0,故④錯誤;
<0,故④錯誤;
∵OB=OC,
∴OB=﹣c,
∴點B坐標為(﹣c,0),
∴ac2﹣bc+c=0,
∴ac﹣b+1=0,
∴ac=b﹣1,故③正確;
∵A(﹣2,0),B(﹣c,0),拋物線線y=ax2+bx+c與x軸交于A(﹣2,0)和B(﹣c,0)兩點,
∴2c= ![]() ,
,
∴2= ![]() ,
,
∴a= ![]() ,故②正確;
,故②正確;
∵ac﹣b+1=0,
∴b=ac+1,a= ![]() ,
,
∴b= ![]() c+1
c+1
∴2b﹣c=2,故①正確;
故答案為:C.
圖像交y軸于負半軸,因此c<0,對稱軸x=![]() <0,可知a、b同號,開口向上,a>0,因此b>0,
<0,可知a、b同號,開口向上,a>0,因此b>0, ![]() <0,故④錯誤;由OB=OC,得OB=﹣c,
<0,故④錯誤;由OB=OC,得OB=﹣c,
點B坐標為(﹣c,0),ac2﹣bc+c=0,c不等于0,同除以c,ac﹣b+1=0,故③正確;再把A(﹣2,0)代入解析式,得4a-2b+c=0,代換b=ac+1,可得4a-2ac-2+c=0,2a(2-c)+(c-2)=0,(c-2)(1-2a)=0,c-2不會等于0,因此a=![]() ,故②正確;把a=
,故②正確;把a=![]() 代入ac﹣b+1=0中,得2b﹣c=2,故①正確,故答案為:C.
代入ac﹣b+1=0中,得2b﹣c=2,故①正確,故答案為:C.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c與x軸交于兩點A(﹣4,0)和B(1,0),與y軸交于點C(0,2),動點D沿△ABC的邊AB以每秒2個單位長度的速度由起點A向終點B運動,過點D作x軸的垂線,交△ABC的另一邊于點E,將△ADE沿DE折疊,使點A落在點F處,設點D的運動時間為t秒.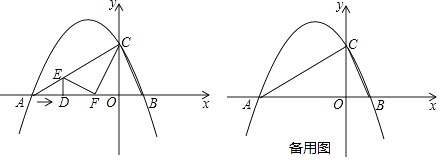
(1)求拋物線的解析式和對稱軸;
(2)是否存在某一時刻t,使得△EFC為直角三角形?若存在,求出t的值;若不存在,請說明理由;
(3)設四邊形DECO的面積為s,求s關于t的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小東家與學校之間是一條筆直的公路,早飯后,小東步行前往學校,途中發現忘帶畫板,停下給媽媽打電話,媽媽接到電話后,帶上畫板馬上趕往學校,同時小東沿原路返回,兩人相遇后,小東立即趕往學校,媽媽沿原路返回16min到家,再過5min小東到達學校,小東始終以100m/min的速度步行,小東和媽媽的距離y(單位:m)與小東打完電話后的步行時間t(單位:min)之間的函數關系如圖所示,下列四種說法:
①打電話時,小東和媽媽的距離為1400米;
②小東和媽媽相遇后,媽媽回家速度為50m/min;
③小東打完電話后,經過27min到達學校;
④小東家離學校的距離為2900m.
其中正確的個數是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)計算:(![]() ﹣
﹣![]() )2+(2
)2+(2![]() +
+![]() )(2
)(2![]() ﹣
﹣![]() )
)
(2)因式分解:9a2(x﹣y)+4b2(y﹣x)
(3)先化簡,再求值:![]() ÷(a﹣1﹣
÷(a﹣1﹣![]() ),其中a2﹣a﹣6=0.
),其中a2﹣a﹣6=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC⊥x軸于點A,點B在y軸的正半軸上,∠ABC=60°,AB=4,BC=2 ![]() ,點D為AC與反比例函數y=
,點D為AC與反比例函數y= ![]() 的圖象的交點.若直線BD將△ABC的面積分成1:2的兩部分,則k的值為 .
的圖象的交點.若直線BD將△ABC的面積分成1:2的兩部分,則k的值為 . 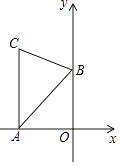
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD沿對角線AC翻折,點B落在點F處,FC交AD于E.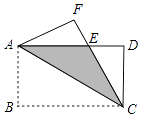
(1)求證:△AFE≌△CDE;
(2)若AB=4,BC=8,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,線段AB的長為10cm,點D是AB上的一個動點,不與點A重合,以AD為邊作等邊△ACD,過點D作DP⊥CD,過DP上一動點G(不與點D重合)作矩形CDGH,對角線交于點O,連接OA、OB,則線段OB的最小值是________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com