
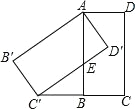
【題目】如圖,將矩形ABCD繞點A順時針旋轉,得到矩形AB′C′D′,點 C的對應點 C′恰好落在CB的延長線上,邊AB交邊 C′D′于點E.
(1)求證:BC=BC′;
(2)若 AB=2,BC=1,求AE的長.
【答案】(1)證明見解析;(2)AE=![]() .
.
【解析】
(1)連結 AC、AC′,根據矩形的性質得到∠ABC=90°,即 AB⊥CC′, 根據旋轉的性質即可得到結論;
(2)根據矩形的性質得到 AD=BC,∠D=∠ABC′=90°,根據旋轉的性質得到 BC′=AD′,AD=AD′,證得 BC′=AD′,根據全等三角形的性質得到 BE=D′E,設 AE=x,則 D′E=2﹣x,根據勾股定理列方程即可得到結論.
解::(1)連結 AC、AC′,
∵四邊形 ABCD為矩形,
∴∠ABC=90°,即 AB⊥CC′,
∵將矩形 ABCD 繞點A順時針旋轉,得到矩形 AB′C′D′,
∴AC=AC′,
∴BC=BC′;
(2)∵四邊形 ABCD 為矩形,
∴AD=BC,∠D=∠ABC′=90°,
∵BC=BC′,
∴BC′=AD′,
∵將矩形 ABCD 繞點 A 順時針旋轉,得到矩形 AB′C′D′,
∴AD=AD′,
∴BC′=AD′,
在△AD′E 與△C′BE中
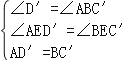
∴△AD′E≌△C′BE,
∴BE=D′E,
設 AE=x,則 D′E=2﹣x,
在 Rt△AD′E 中,∠D′=90°,
由勾定理,得 x2﹣(2﹣x)2=1,
解得 x=![]() ,
,
∴AE= ![]() .
.


科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系xOy中的圖形W和點P,給出如下定義:F為圖形W上任意一點,將P,F兩點間距離的最小值記為m,最大值記為M,稱M與m的差為點P到圖形W的“差距離”,記作d(P,W),即d(P,W)=M-m,已知點A(2,1),B(-2,1)
(1)求d(O,AB);
(2)點C為直線y=1上的一個動點,當d(C,AB)=1時,點C的橫坐標是 ;
(3)點D為函數y=x+b(-2≤x≤2)圖象上的任意一點,當d(D,AB)≤2時,直接寫出b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有一列數:![]() ,
,![]() ,0,-22,-(+2),-(-4),請回答下列問題:
,0,-22,-(+2),-(-4),請回答下列問題:
(1)其中非負整數是_______________;(2)到原點距離相等的數是________________;
(3)畫出數軸,并在數軸上表示這一列數,再用“<”連接起來.
查看答案和解析>>
科目:初中數學 來源: 題型:
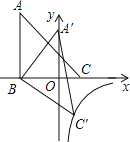
【題目】如圖,△ABC的三個頂點的坐標分別為A(﹣3,5),B(﹣3,0),C(2,0),將△ABC繞點B順時針旋轉一定角度后使A落在y軸上,與此同時頂點C恰好落在y=![]() 的圖象上,則k的值為__.
的圖象上,則k的值為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
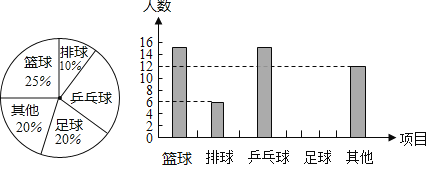
【題目】某課外研究小組為了解學生參加課外體育活動的情況,采取抽樣調查的方法從籃球、排球、乒乓球、足球及其他等五個方面調查了若干名同學的興趣愛好(每人只能選其中一項),并將調查結果繪制成統計圖,請根據圖中提供的信息解答下列問題:
(1)在這次考察中一共調查了 名學生,請補全條形統計圖;
(2)被調查同學中恰好有5名學來自初一12班,其中有2名同學選擇了籃球,有3名同學選擇了乒乓球,曹老師打算從這5名同學中選擇兩同學了解他們對體育社團的看法,請用列表法或畫樹狀圖法,求選出的兩人恰好為一人選擇籃球、一人選擇乒乓球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,□ABCD的頂點坐標分別為A(3.6,a),B(2,2),C(b,3.4),D(8,6),則![]() 的值為( )
的值為( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】沙坪壩區政府決定從2014年11月起到2016年底,兩年時間創建成為國家衛生城區,轄區內企業的污水處理通常有兩種方式,一種是輸送到污水廠進行集中處理,另一種是通過企業的自身設備進行處理,某企業每月的污水量均為2500噸,數量巨大需要兩種處理方式同時進行.由于企業自身設備老化等問題,2015年每月自身處理污水量y(噸)與月份x(x取整數)之間滿足的函數關系式為y=2500﹣100x,該企業自身處理每噸污水的成本為4元,其余部分由污水廠統一處理,污水廠收取企業每噸污水處理費10元
(1)該企業2015年哪幾個月用于污水處理的費用不超過12000元?
(2)2016年以來,由于該企業自建污水處理設備的全面運行,該企業決定擴大產能并將所有污水全部自身處理,估計擴大產能后2016年每月的污水量都將在2015年每月的基礎上增加a%,同時每噸污水處理的費用將在每噸4元的基礎上增加5(a﹣30)%,為鼓勵節能降耗,減輕企業負擔,財政對企業處理污水的費用進行50%的補助,若該企業每月的污水處理費用為8437.5元,請計算出a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】足球運動員將足球沿與地面成一定角度的方向踢出,足球飛行的路線是一條拋物線,不考慮空氣阻力,足球距離地面的高度![]() (單位:
(單位:![]() )與足球被踢出后經過的時間
)與足球被踢出后經過的時間![]() (單位:
(單位:![]() )之間的關系如下表:
)之間的關系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列結論:①足球距離地面的最大高度為![]() ;②足球飛行路線的對稱軸是直線
;②足球飛行路線的對稱軸是直線![]() ;③足球被踢出
;③足球被踢出![]() 時落地;④足球被踢出
時落地;④足球被踢出![]() 時,距離地面的高度是
時,距離地面的高度是![]() .
.
其中正確結論的個數是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】樹葉有關的問題
如圖,一片樹葉的長是指沿葉脈方向量出的最長部分的長度(不含葉柄),樹葉的寬是指沿與主葉脈垂直方向量出的最寬處的長度,樹葉的長寬比是指樹葉的長與樹葉的寬的比值。

某同學在校園內隨機收集了A樹、B樹、C樹三棵的樹葉各10片,通過測量得到這些樹葉的長y(單位:cm),寬x(單位:cm)的數據,計算長寬比,理如下:
表1 A樹、B樹、C樹樹葉的長寬比統計表
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
A樹樹葉的長寬比 | 4.0 | 4.9 | 5.2 | 4.1 | 5.7 | 8.5 | 7.9 | 6.3 | 7.7 | 7.9 |
B樹樹葉的長寬比 | 2.5 | 2.4 | 2.2 | 2.3 | 2.0 | 1.9 | 2.3 | 2.0 | 1.9 | 2.0 |
C樹樹葉的長寬比 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.0 | 1.1 | 0.9 | 1.0 | 1.3 |
表1 A樹、B樹、C樹樹葉的長寬比的平均數、中位數、眾數、方差統計表
平均數 | 中位數 | 眾數 | 方差 | |
A樹樹葉的長寬比 | 6.2 | 6.0 | 7.9 | 2.5 |
B樹樹葉的長寬比 | 2.2 | 0.38 | ||
C樹樹葉的長寬比 | 1.1 | 1.1 | 1.0 | 0.02 |
A樹、B樹、C樹樹葉的長隨變化的情況

解決下列問題:
(1)將表2補充完整;
(2)①小張同學說:“根據以上信息,我能判斷C樹樹葉的長、寬近似相等。”
②小李同學說:“從樹葉的長寬比的平均數來看,我認為,下圖的樹葉是B樹的樹葉。”
![]()
請你判斷上面兩位同學的說法中,誰的說法是合理的,誰的說法是不合理的,并給出你的理由;
(3)現有一片長103cm,寬52cm的樹葉,請將該樹葉的數用“★”表示在圖1中,判斷這片樹葉更可能來自于A、B、C中的哪棵樹?并給出你的理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com