
【題目】在平面直角坐標(biāo)系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X軸上的一點(diǎn),Q是Y軸上的一點(diǎn),若以點(diǎn)A,B,P,Q四個點(diǎn)為頂點(diǎn)的四邊形是平行四邊形,則Q點(diǎn)的坐標(biāo)是 .
【答案】(0,﹣6)或(0,﹣2)或(0,6)
【解析】解:如圖所示, 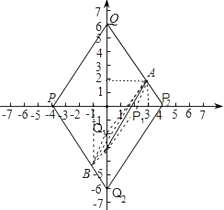
當(dāng)AB為邊,①即當(dāng)四邊形ABQ2P2是平行四邊形,所以AB=P2Q2 , AP2=BQ2 ,
∴Q2點(diǎn)的坐標(biāo)是:(0,﹣6),
②當(dāng)四邊形QPBA是平行四邊形,所以AB=PQ,QA=PB,
∴Q點(diǎn)的坐標(biāo)是:(0,6),
當(dāng)AB為對角線,即當(dāng)四邊形P1AQ1B是平行四邊形,所以AP1=Q1B,
AQ1=BP1 ,
∴Q1點(diǎn)的坐標(biāo)是:(0,﹣2).
故答案為:(0,﹣6)或(0,﹣2)或(0,6).
如圖,當(dāng)AB為邊,①當(dāng)四邊形ABQ2P2是平行四邊形,所以AB=P2Q2 , AP2=BQ2 , ②當(dāng)四邊形QPBA是平行四邊形,所以AB=PQ,QA=PB,當(dāng)AB為對角線,即當(dāng)四邊形P1AQ1B是平行四邊形,所以AP1=Q1B,AQ1=BP1 , 結(jié)合圖形分別得出即可.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC內(nèi)接于⊙O,∠A的度數(shù)為60°,∠ABC、∠ACB的角平分線分別交于AC、AB于點(diǎn)D、E,CE、BD相交于點(diǎn)F.以下四個結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中結(jié)論一定正確的序號數(shù)是( )
.其中結(jié)論一定正確的序號數(shù)是( )

A. ①② B. ①③ C. ③④ D ②④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AD是圓O的切線,切點(diǎn)為A,AB是圓O的弦。過點(diǎn)B作BC//AD,交圓O于點(diǎn)C,連接AC,過點(diǎn)C作CD//AB,交AD于點(diǎn)D。連接AO并延長交BC于點(diǎn)M,交過點(diǎn)C的直線于點(diǎn)P,且BCP=ACD。
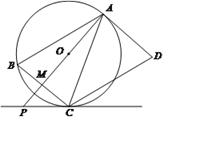
(1) 判斷直線PC與圓O的位置關(guān)系,并說明理由:
(2) 若AB=9,BC=6,求PC的長。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列二次函數(shù)中,圖象以直線x=2為對稱軸、且經(jīng)過點(diǎn)(0,1)的是( )
A.y=(x﹣2)2+1
B.y=(x+2)2+1
C.y=(x﹣2)2﹣3
D.y=(x+2)2﹣3
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
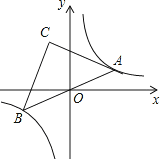
【題目】如圖,點(diǎn)A是雙曲線y=![]() 在第一象限上的一動點(diǎn),連接AO并延長交另一分支于點(diǎn)B,以AB為斜邊作等腰Rt△ABC,點(diǎn)C在第二象限,隨著點(diǎn)A的運(yùn)動,點(diǎn)C的位置也不斷的變化,但始終在一函數(shù)圖象上運(yùn)動,則這個函數(shù)的解析式為 .
在第一象限上的一動點(diǎn),連接AO并延長交另一分支于點(diǎn)B,以AB為斜邊作等腰Rt△ABC,點(diǎn)C在第二象限,隨著點(diǎn)A的運(yùn)動,點(diǎn)C的位置也不斷的變化,但始終在一函數(shù)圖象上運(yùn)動,則這個函數(shù)的解析式為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,點(diǎn)(1,-5)所在象限是 ( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com