
【題目】如圖,在△ABC中,∠ABC=90°,BD為AC邊上的中線,過點C作CE⊥BD于點E,過點A作BD的平行線,交CE的延長線于點F,在AF的延長線上截取FG=BD,連接BG、DF.若AG=13,BG=5,則CF的長為__.

科目:初中數學 來源: 題型:
【題目】如圖,點A(1,6)和點B在反比例函數圖象上,AD⊥x軸于點D,BC⊥x軸于點C,DC=5. 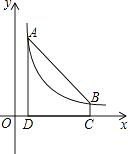
(1)求反比例函數的表達式和點B的坐標;
(2)連接AB,在線段DC上是否存在一點E,使△ABE的面積等于5?若存在,求出點E的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠BAD=60°,點M是AB的中點,P是對角線AC上的一個動點,若PM+PB的最小值是9,則AB的長是( ) 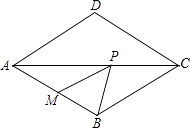
A.6 ![]()
B.3 ![]()
C.9
D.4.5
查看答案和解析>>
科目:初中數學 來源: 題型:
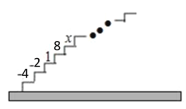
【題目】如圖,階梯圖的每個臺階上都標著一個數,從下到上的第1個至第4個臺階上依次標著﹣4,﹣2,1,8,且任意相鄰四個臺階上數的和都相等.
嘗試:(1)求前4個臺階上數的和是多少?
(2)求第5個臺階上的數x是多少?
應用: 求從下到上39個臺階上數的和.
發現:試用含k(k為正整數)的代數式表示出數“1”所在的臺階數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,△ABC中,∠A=90°,D是AC上一點,且∠ADB=2∠C,P是BC上任一點,PE⊥BD于點E,PF⊥AC于點F,下列結論:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.
其中結論正確的個數是( )
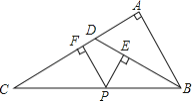
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按圖中所示方法將△BCD沿BD折疊,使點C落在AB邊的C′點,那么△ADC′的面積是( ) 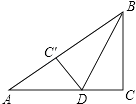
A.3cm2
B.4cm2
C.5cm2
D.6cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,正方形OABC的兩邊OA、OC分別落在x軸、y軸的正半軸上,等腰Rt△ADE的兩個頂點D、E和正方形頂點B三點在一條直線上.
(1)如圖1,連接OD,求證:△OAD≌△BAE;
(2)如圖2,連接CD,求證:BE﹣![]() DE=
DE=![]() CD;
CD;
(3)如圖3,當圖1中的Rt△ADE的頂點D與點B重合時,點E正好落在x軸上,F為線段OC上一動點(不與O、C重合),G為線段AF的中點,若CG⊥GK交BE于點K時,請問∠KCG的大小是否變化?若不變,請求其值;若改變,求出變化的范圍.
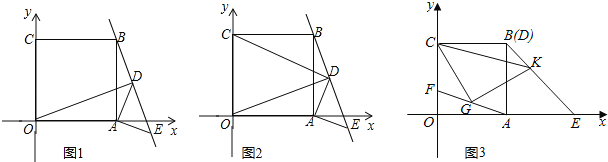
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一次函數y=kx+b的圖象如圖所示,則k,b的值可能為( )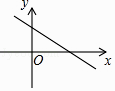
A.k=3,b=3
B.k=3,b=﹣3
C.k=﹣3,b=3
D.k=﹣3,b=﹣3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD平分∠BAC,過AD的中點O作EF⊥AD,分別交AB、AC于點E、F,連接DE、DF. 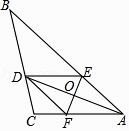
(1)判斷四邊形AFDE是什么四邊形?請說明理由;
(2)若BD=8,CD=3,AE=4,求CF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com