
【題目】某養(yǎng)豬場(chǎng)對(duì)豬舍進(jìn)行噴藥消毒.在消毒的過(guò)程中,先經(jīng)過(guò)![]() 的藥物集中噴灑,再封閉豬舍
的藥物集中噴灑,再封閉豬舍![]() ,然后再打開(kāi)窗戶進(jìn)行通風(fēng).已知室內(nèi)每立方米空氣中含藥量
,然后再打開(kāi)窗戶進(jìn)行通風(fēng).已知室內(nèi)每立方米空氣中含藥量![]() (
(![]() )與藥物在空氣中的持續(xù)時(shí)間
)與藥物在空氣中的持續(xù)時(shí)間![]() (
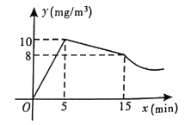
(![]() )之間的函數(shù)圖象如圖所示,其中在打開(kāi)窗戶通風(fēng)前
)之間的函數(shù)圖象如圖所示,其中在打開(kāi)窗戶通風(fēng)前![]() 與
與![]() 分別滿足兩個(gè)一次函數(shù),在通風(fēng)后
分別滿足兩個(gè)一次函數(shù),在通風(fēng)后![]() 與
與![]() 滿足反比例函數(shù).
滿足反比例函數(shù).
(1)求反比例函數(shù)的關(guān)系式;
(2)當(dāng)豬舍內(nèi)空氣中含藥量不低于![]() 且持續(xù)時(shí)間不少于
且持續(xù)時(shí)間不少于![]() ,才能有效殺死病毒,問(wèn)此次消毒是否有效?
,才能有效殺死病毒,問(wèn)此次消毒是否有效?
【答案】(1)![]() ;(2)此次消毒能有效殺死該病毒.
;(2)此次消毒能有效殺死該病毒.
【解析】
(1)用待定系數(shù)法求函數(shù)解析式;
(2)求正比例函數(shù)解析式,計(jì)算正比例函數(shù)和反比例函數(shù)的函數(shù)值為5對(duì)應(yīng)的自變量的值,則它們的差為含藥量不低于5mg/m3的持續(xù)時(shí)間,然后與21比較大小即可判斷此次消毒是否有效.
解:(1)設(shè)反比例函數(shù)關(guān)系式為![]() .
.
∵反比例函數(shù)的圖像過(guò)點(diǎn)![]() ,
,
∴![]() .
.
∴![]() .
.
(2)設(shè)正比例函數(shù)關(guān)系式為![]() .
.
把![]() ,
,![]() 代入上式,得
代入上式,得![]() .
.
∴![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() .
.
把![]() 代入
代入![]() ,得
,得![]() .
.
∴![]() .
.
答:此次消毒能有效殺死該病毒.



 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:在![]() 中,
中,![]() ,線段
,線段![]() 的垂直平分線交
的垂直平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,且
上,且![]() ,連接
,連接![]()
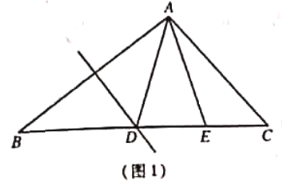
![]() 如圖1 ,求證:
如圖1 ,求證:![]()
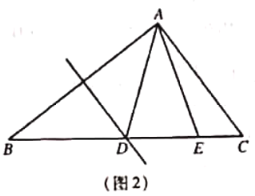
![]() 如圖2,當(dāng)
如圖2,當(dāng)![]() 時(shí).在不添加任何輔助線情況下,請(qǐng)直接寫(xiě)出圖2中的四個(gè)等腰三角形.
時(shí).在不添加任何輔助線情況下,請(qǐng)直接寫(xiě)出圖2中的四個(gè)等腰三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
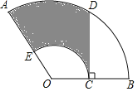
【題目】如圖,扇形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() ⊥
⊥![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,以
,以![]() 為半徑的
為半徑的![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,則圖中陰影部分的面積是___.
,則圖中陰影部分的面積是___.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
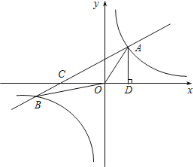
【題目】如圖,在平面直角坐標(biāo)系中,一次函數(shù)![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖象相交于
的圖象相交于![]() 兩點(diǎn),過(guò)點(diǎn)
兩點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() .
.
(1)求一次函數(shù)和反比例函數(shù)的表達(dá)式;
(2)求![]() 的面積;
的面積;
(3)![]() 是
是![]() 軸上一點(diǎn),且
軸上一點(diǎn),且![]() 是等腰三角形,請(qǐng)直接寫(xiě)出所有符合條件的
是等腰三角形,請(qǐng)直接寫(xiě)出所有符合條件的![]() 點(diǎn)坐標(biāo).
點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,該拋物線是由y=x2平移后得到,它的頂點(diǎn)坐標(biāo)為(﹣![]() ,﹣
,﹣![]() ),并與坐標(biāo)軸分別交于A,B,C三點(diǎn).
),并與坐標(biāo)軸分別交于A,B,C三點(diǎn).
(1)求A,B的坐標(biāo).
(2)如圖2,連接BC,AC,在第三象限的拋物線上有一點(diǎn)P,使∠PCA=∠BCO,求點(diǎn)P的坐標(biāo).
(3)如圖3,直線y=ax+b(b<0)與該拋物線分別交于P,G兩點(diǎn),連接BP,BG分別交y軸于點(diǎn)D,E.若ODOE=3,請(qǐng)?zhí)剿?/span>a與b的數(shù)量關(guān)系.并說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
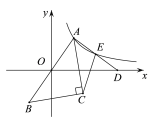
【題目】如圖,點(diǎn)A與點(diǎn)B關(guān)于原點(diǎn)對(duì)稱,點(diǎn)C在第四象限,∠ACB=90°.點(diǎn)D是![]() 軸正半軸上一點(diǎn),AC平分∠BAD,E是AD的中點(diǎn),反比例函數(shù)
軸正半軸上一點(diǎn),AC平分∠BAD,E是AD的中點(diǎn),反比例函數(shù)![]() (
(![]() )的圖象經(jīng)過(guò)點(diǎn)A,E.若△ACE的面積為6,則
)的圖象經(jīng)過(guò)點(diǎn)A,E.若△ACE的面積為6,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)于任意一個(gè)四位數(shù),我們可以記為![]() ,即
,即![]() .若規(guī)定: 對(duì)四位正整數(shù)
.若規(guī)定: 對(duì)四位正整數(shù)![]() 進(jìn)行 F運(yùn)算,得到整數(shù)
進(jìn)行 F運(yùn)算,得到整數(shù)![]() .例如,
.例如,![]() ;
;![]() .
.
(1)計(jì)算:![]() ;
;
(2)當(dāng)![]() 時(shí),證明:
時(shí),證明:![]() 的結(jié)果一定是4的倍數(shù);
的結(jié)果一定是4的倍數(shù);
(3)求出滿足![]() 的所有四位數(shù).
的所有四位數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
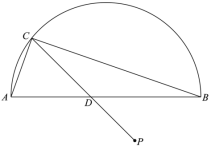
【題目】如圖,![]() 是半圓的直徑,P是半圓與直徑
是半圓的直徑,P是半圓與直徑![]() 所圍成的圖形的外部的一定點(diǎn),D是直徑
所圍成的圖形的外部的一定點(diǎn),D是直徑![]() 上一動(dòng)點(diǎn),連接
上一動(dòng)點(diǎn),連接![]() 并延長(zhǎng),交半圓于點(diǎn)C,連接
并延長(zhǎng),交半圓于點(diǎn)C,連接![]() .已知
.已知![]() ,設(shè)
,設(shè)![]() 兩點(diǎn)間的距離為
兩點(diǎn)間的距離為![]() ,
,![]() 兩點(diǎn)之間的距離為
兩點(diǎn)之間的距離為![]() 兩點(diǎn)之間的距離為
兩點(diǎn)之間的距離為![]() .
.
小明根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),分別對(duì)函數(shù)![]() 隨自變量x的變化而變化的規(guī)律進(jìn)行了探究.
隨自變量x的變化而變化的規(guī)律進(jìn)行了探究.
下面是小明的探究過(guò)程,請(qǐng)補(bǔ)充完整:
(1)按照下表自變量x的值進(jìn)行取點(diǎn)、畫(huà)圖、測(cè)量,分別得到![]() 與x的幾組對(duì)應(yīng)值;
與x的幾組對(duì)應(yīng)值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
(2)在同一平面直角坐標(biāo)系![]() 中,描出補(bǔ)全后的表中各組數(shù)值所對(duì)應(yīng)的點(diǎn)
中,描出補(bǔ)全后的表中各組數(shù)值所對(duì)應(yīng)的點(diǎn)![]() ,
,![]() ,并畫(huà)出函數(shù)
,并畫(huà)出函數(shù)![]() 的圖象;
的圖象;
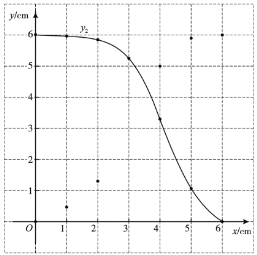
(3)結(jié)合函數(shù)圖象,解決問(wèn)題:當(dāng)![]() 有一個(gè)角的正弦值為
有一個(gè)角的正弦值為![]() 時(shí),
時(shí),![]() 的長(zhǎng)約為_____cm.
的長(zhǎng)約為_____cm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某扶貧工作隊(duì)為一貧困戶提供了![]() 萬(wàn)元的無(wú)息脫貧貸款.該貧困戶利用這筆貸款,注冊(cè)了一家網(wǎng)店,銷(xiāo)售一種成本價(jià)為
萬(wàn)元的無(wú)息脫貧貸款.該貧困戶利用這筆貸款,注冊(cè)了一家網(wǎng)店,銷(xiāo)售一種成本價(jià)為![]() 元/件的農(nóng)產(chǎn)品.已知銷(xiāo)售價(jià)高于成本價(jià),且不高于
元/件的農(nóng)產(chǎn)品.已知銷(xiāo)售價(jià)高于成本價(jià),且不高于![]() 元/件,網(wǎng)店每月需支付電費(fèi)等其它費(fèi)用
元/件,網(wǎng)店每月需支付電費(fèi)等其它費(fèi)用![]() 千元市場(chǎng)調(diào)查發(fā)現(xiàn),該農(nóng)產(chǎn)品每月銷(xiāo)售量為
千元市場(chǎng)調(diào)查發(fā)現(xiàn),該農(nóng)產(chǎn)品每月銷(xiāo)售量為![]() (百件)與銷(xiāo)售價(jià)
(百件)與銷(xiāo)售價(jià)![]() (元/件)之間的函數(shù)關(guān)系如圖所示
(元/件)之間的函數(shù)關(guān)系如圖所示
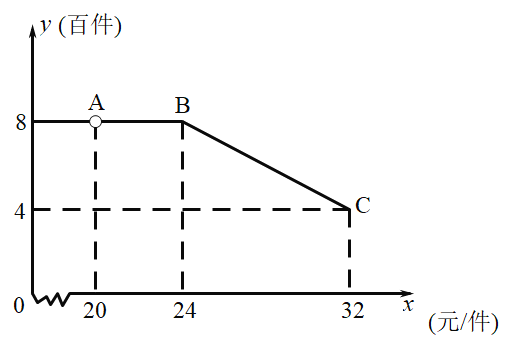
(1)求該網(wǎng)店每月利潤(rùn)![]() (百元)與銷(xiāo)售價(jià)
(百元)與銷(xiāo)售價(jià)![]() (元/件)之間的函數(shù)關(guān)系式,并注明自變量
(元/件)之間的函數(shù)關(guān)系式,并注明自變量![]() 的取值范圍:
的取值范圍:
(2)該貧困戶從網(wǎng)店開(kāi)業(yè)起,最快在第幾個(gè)月可用銷(xiāo)售利潤(rùn)還清無(wú)息貸款?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com