
【題目】如圖,已知![]() 內接于⊙
內接于⊙![]() ,直徑
,直徑![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() .過點
.過點![]() 作⊙
作⊙![]() 的切線,交
的切線,交![]() 的延長線于點
的延長線于點![]() .
.
(1)若![]() ,求
,求![]() 的度數;
的度數;
(2)若![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,連接![]() ,設
,設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,若
,若![]() ,求
,求![]() 的值
的值
【答案】(1)50°;(2)詳見解析;(3)![]()
【解析】
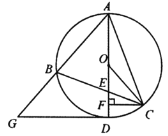
(1)連接BD,如圖,利用切線性質和圓周角定理得到∠ADG=∠ABD=90°,再利用等角的余角相等得到∠ADB=∠G=50°,然后根據圓周角定理得到∠ACB的度數;
(2)連接CD,如圖,利用等腰三角形的性質得到∠ABE=∠AEB,∠ODC=∠OCD,再利用圓周角定理得到∠ABC=∠ADC,然后根據三角形內角和可判斷∠BAD=∠DOC;
(3)先證明△ABD∽△OFC得到![]() ,設
,設![]() 則
則![]() 則利用三角形面積公式得到
則利用三角形面積公式得到![]() 則可設OF=4k,則OA=5k,利用勾股定理計算出CF,然后根據正切的定義求解.
則可設OF=4k,則OA=5k,利用勾股定理計算出CF,然后根據正切的定義求解.
(1)解:連接BD,如圖,
∵DG為切線,
∴AD⊥DG, ∴∠ADG=90°,
∵AD為直徑, ∴∠ABD=90°,
![]() ∠GDB+∠G=90°,∠ADB+∠GDB=90°,
∠GDB+∠G=90°,∠ADB+∠GDB=90°,
∴∠ADB=∠G=50°,
∴∠ACB=∠ADB=50°;
(2)證明:連接CD,如圖,
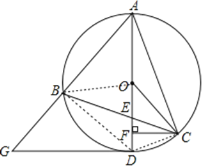
∵AB=AE, ∴∠ABE=∠AEB,
∵OD=OC, ∴∠ODC=∠OCD,
而∠ABC=∠ADC, ∴∠ABE=∠AEB=∠ODC=∠OCD,
∴∠BAD=∠FOC;
(3)解:∵∠BAD=∠FOC,∠ABD=∠OFC,
∴△ABD∽△OFC,
∴![]() ,
,
∵ ![]()
設![]() 則
則![]()
∴![]()
∴![]()
∵![]()
∴設OF=4k,則OA=5k,
在Rt△OCF中,OC=5k, CF=![]()
∴tan∠CAF=![]()


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:初中數學 來源: 題型:
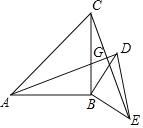
【題目】如圖,△ABC和△BED都是等腰直角三角形,∠ABC=∠DBE=90°,AD,CE相交于點G
(1)求證:△ABD≌△CBE;
(2)求證:AD⊥CE;
(3)連接AE,CD,若AE=![]() CD=5,求△ABC和△BED的面積之和.
CD=5,求△ABC和△BED的面積之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
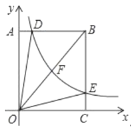
【題目】如圖,反比例函數![]() 的圖象分別與矩形
的圖象分別與矩形![]() 的邊
的邊![]() ,
,![]() 相交于點
相交于點![]() ,
,![]() ,與對角線
,與對角線![]() 交于點
交于點![]() ,以下結論:
,以下結論:
①若![]() 與
與![]() 的面積和為2,則
的面積和為2,則![]() ;
;
②若![]() 點坐標為
點坐標為![]() ,
,![]() ,則
,則![]() ;
;
③圖中一定有![]() ;
;
④若點![]() 是
是![]() 的中點,且
的中點,且![]() ,則四邊形
,則四邊形![]() 的面積為18.
的面積為18.
其中一定正確個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
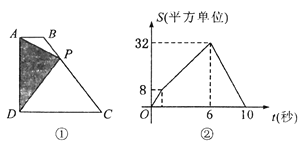
【題目】如圖①,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 從
從![]() 點出發,以每秒2個單位長度的速度,按
點出發,以每秒2個單位長度的速度,按![]() 的順序在邊上勻速運動,設
的順序在邊上勻速運動,設![]() 點的運動時間為
點的運動時間為![]() 秒,
秒,![]() 的面積為
的面積為![]() ,
,![]() 關于
關于![]() 的函數圖像如圖②所示,當
的函數圖像如圖②所示,當![]() 運動到
運動到![]() 中點時,
中點時,![]() 的面積為__________.
的面積為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解全校學生到校上學的方式,在全校隨機抽取了若干名學生進行問卷調查,問卷給出了四種上學方式供學生選擇,每人只能選一項,且不能不選.將調查得到的結果繪制成如圖所示的扇形統計圖和條形統計圖(均不完整).

根據以上信息,解答下列問題:
(1)在這次調查中,一共抽取了 名學生;
(2)補全條形統計圖;
(3)如果全校有1200名學生,學習準備的400個自行車停車位是否夠用?
查看答案和解析>>
科目:初中數學 來源: 題型:
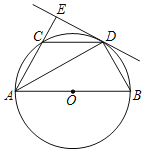
【題目】如圖,AB是⊙O的直徑,C點在⊙O上,AD平分∠BAC交⊙O于D,過D作直線AC的垂線,交AC的延長線于E,連接BD,CD.
(1)求證:直線DE是⊙O的切線;
(2)若直徑AB=6,填空:
①當AD= 時,四邊形ACDO是菱形;
②過D作DH⊥AB,垂足為H,當AD= 時,四邊形AHDE是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形紙片ABCD的邊長為12,E是邊CD的中點,連接AE,折疊該紙片,使點A落在AE上的G點,并使折痕經過點B,得到折痕BF,點F在AD上,若DE=5,則GE的長為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著人們“節能環保,綠色出行”意識的增強,越來越多的人喜歡騎自行車出行,也給自行車商家帶來商機.某自行車行經營的A型自行車去年銷售總額為8萬元.今年該型自行車每輛售價預計比去年降低200元.若該型車的銷售數量與去年相同,那么今年的銷售總額將比去年減少10%,求:
(1)A型自行車去年每輛售價多少元?
(2)該車行今年計劃新進一批A型車和新款B型車共60輛,且B型車的進貨數量不超過A型車數量的兩倍.已知,A型車和B型車的進貨價格分別為1500元和1800元,計劃B型車銷售價格為2400元,應如何組織進貨才能使這批自行車銷售獲利最多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com