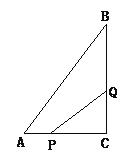
【題目】如圖4所示，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，點P從點A出發沿邊AC向點C以1cm/s的速度移動，點Q從C點出發沿CB邊向點B以2cm/s的速度移動.
(1)、如果P、Q同時出發，幾秒鐘后，可使△PCQ的面積為8平方厘米？
(2)、點P、Q在移動過程中，是否存在某一時刻，使得△PCQ的面積等于△ABC的面積的一半.若存在，求出運動的時間；若不存在，說明理由.
【答案】(1)、2s或4s；(2)、不存在
【解析】
試題分析：(1)設時間為x，則分別用含x的代數式表示PC和CQ的長度，根據三角形面積的計算公式求出x的值；(2)、方法同第一個.
試題解析：(1)設xs后，可使△PCQ的面積為8
，所以 AP＝xcm，PC＝(6－x)cm，CQ＝2xcm.
則根據題意，得
·(6－x)·2x＝8.整理，得
－6x+8＝0
解得
＝2，
＝4.
所以P、Q同時出發，2s或4s后可使△PCQ的面積為8.
(2)、設點P出發x秒后，△PCQ的面積等于△ABC面積的一半.
則根據題意，得(6－x)·2x＝××6×8.整理，得－6x+12＝0.
由于此方程沒有實數根，所以不存在使△PCQ的面積等于△ABC面積一半的時刻.
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=ax2+bx+c（a≠0）交x軸于A（﹣1，0），B（5，0）兩點，與y軸交于點C（0，2）
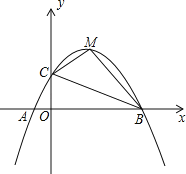
（1）求拋物線的解析式；
（2）若點M為拋物線的頂點，連接BC、CM、BM，求△BCM的面積；
（3）連接AC，在x軸上是否存在點P使△ACP為等腰三角形？若存在，請求出點P的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】七年級（2）班派出12名同學參加數學競賽，老師以75分為基準，把分數超過75分的部分記為正數，不足的部分記為負數．評分記錄如下：
+15，+20，-5，-4，-3，+4，+6，+2，+3，+5，+7，-8
（1）這12名同學中最高分和最低分各是多少分？
（2）超過基準分的有多少人？
（3）這12名同學的平均成績是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
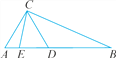
【題目】如圖，在△ABC中，AD＝AC，BE＝BC.
(1)若∠ACB＝96°，求∠DCE的度數．
(2)問：∠DCE與∠A，∠B之間存在怎樣的數量關系(直接寫出答案)?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下圖是由一些火柴棒搭成的圖案：
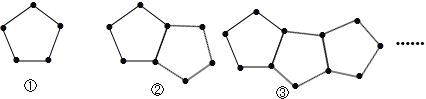
（1）擺第①個圖案用 根火柴棒，擺第②個圖案用 根火柴棒，擺第③個圖案用 根火柴棒．
（2）按照這種方式擺下去，擺第n個圖案用多少根火柴棒？
（3）計算一下擺121根火柴棒時，是第幾個圖案？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某學校準備食建一個面積為200m2的矩形花圃，它的長比寬多10m，設花圃的寬為x m．則可列方程為（ ）
A.x （x﹣10）=200
B.2x+2 （x﹣10）=200
C.x（x+10）=200
D.2x+2（x+10）=200
查看答案和解析>>
科目：初中數學 來源： 題型：
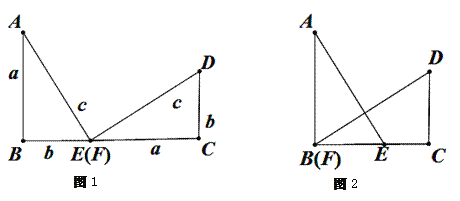
【題目】（1）以a,b為直角邊，c為斜邊作兩個全等的Rt△ABE與Rt△FCD拼成如圖1所示的圖形，使B,E,F,C四點在一條直線上（此時E,F重合），可知△ABE ≌△FCD，AE
DF,請你證明：
;
（2)在（1）中，固定△FCD，再將△ABE沿著BC平移到如圖2的位置(此時B,F重合），請你重新證明：.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】鄭州市霧霾天氣趨于嚴重，丹尼斯商場根據民眾健康需要，代理銷售每臺 進價分別為600元、560元的A、B兩種型號的空氣凈化器，如表是近兩周的銷售情況：
銷售時段 | 銷售數量 | 銷售收入 | |
A種型號 | B種型號 | ||
第一周 | 4臺 | 5臺 | 7100元 |
第二周 | 6臺 | 10臺 | 12600元 |
（進價、售價均保持不變，利潤=銷售收入﹣進貨成本）
（1）求A，B兩種型號的空氣凈化器的銷售單價；
（2）若商場準備用不多于17200元的金額再采購這兩種型號的空氣凈化器共30臺，超市銷售完這30臺空氣凈化器能否實現利潤為6200元的目標，若能，請給出相應的采購方案；若不能，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com