
如圖,拋物線 與直線AB
與直線AB 交于x軸上的一點A,和另一點B(4,n).點P是拋物線A,B兩點間部分上的一個動點(不與點A,B重合),直線PQ與直線AB垂直,交直線AB于點Q.
交于x軸上的一點A,和另一點B(4,n).點P是拋物線A,B兩點間部分上的一個動點(不與點A,B重合),直線PQ與直線AB垂直,交直線AB于點Q.
(1)求拋物線的解析式和cos∠BAO的值。
(2)設點P的橫坐標為 用含
用含 的代數式表示線段PQ的長,并求出線段PQ長的最大值;
的代數式表示線段PQ的長,并求出線段PQ長的最大值;
(3)點E是拋物線上一點,過點E作EF∥AC,交直線AB與點F,若以E、F、A、C為頂點的四邊形為平行四邊形,直接寫出相應的點E的坐標.
(1)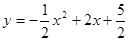 ,
,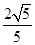 (2)
(2) (3) (
(3) (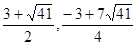 ) (
) (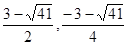 )
)
解析試題分析:解:(1)把y=0代入 得,x=-1,∴A(-1,0),把點B(4,n) 代入
得,x=-1,∴A(-1,0),把點B(4,n) 代入 得
得
n= ,∴B(4,
,∴B(4, )。把A(-1,0)、B(4,
)。把A(-1,0)、B(4, )代入
)代入
得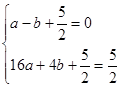 ∴
∴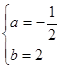
∴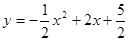
過點B作BH⊥x軸于點H
則BH=2.5,OH=4,∴AH=5,由勾股定理得:
∴co s∠BAO=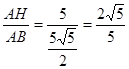
(2)過點P作PM∥y軸交直線AB于點M,
P (m,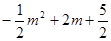 ), M(m,
), M(m, )
)
∴PM=(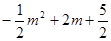 )-(
)-( )
)
=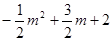
∵∠BAH=∠MPQ,又∵PQ="P" M co s ∠MPQ="PM" co s ∠BAH
=
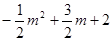 )=
)=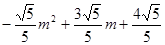
∵ ,∴當m=
,∴當m=
PQ最大值=
(3)(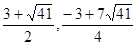 ) (
) (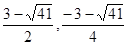 )
)
考點:二次函數與幾何圖形
點評:該題較為復雜,主要考查學生對二次函數解析式的求解方法,以及它在幾何中的應用,建議結合圖像分析。


科目:初中數學 來源: 題型:
 =-1,與x軸交于點C,且∠ABC=90°
=-1,與x軸交于點C,且∠ABC=90°查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,拋物線![]() 與直線y=x+1交于A、C兩點,與y軸交于B,AB∥x軸,且
與直線y=x+1交于A、C兩點,與y軸交于B,AB∥x軸,且![]() , D、E是直線y=x+1與坐標軸的交點,
, D、E是直線y=x+1與坐標軸的交點,
(1)求拋物線的解析式;
(2)在坐標軸上找出所有的點F,使△CEF與△ABD相似,直接寫出它的坐標;
(3)P為x軸上一點,Q為此拋物線上一點,是否存在P,使![]() 得以A、C、P、Q為頂點的四邊形是平行四
得以A、C、P、Q為頂點的四邊形是平行四![]() 邊形?若存在,請求出P點的坐標;若不存在,請說明理由.
邊形?若存在,請求出P點的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源:2013-2014學年安徽蚌埠六中九年級11月階段檢測數學試卷(解析版) 題型:解答題
如圖,拋物線 與直線
與直線 交于C,D兩點,其中點C在y軸上,點D的坐標為
交于C,D兩點,其中點C在y軸上,點D的坐標為 。點P是y軸右側的拋物線上一動點,過點P作
。點P是y軸右側的拋物線上一動點,過點P作 軸于點E,交CD于點F.
軸于點E,交CD于點F.

(1)求拋物線的解析式;
(2)若點P的橫坐標為m,當m為何值時,以O,C,P,F為頂點的四邊形是平行四邊形?請說明理由。
(3)若存在點P,使 ,請直接寫出相應的點P的坐標
,請直接寫出相應的點P的坐標
查看答案和解析>>
科目:初中數學 來源:2013年山東省東營市中考數學模擬試卷(二)(解析版) 題型:解答題
 如圖,拋物線
如圖,拋物線 與直線AB交于點A(-1,0),B(4,
與直線AB交于點A(-1,0),B(4, ).點D是拋物線A,B兩點間部分上的一個動點(不與點A,B重合),直線CD與y軸平行,交直線AB于點C,連接AD,BD.
).點D是拋物線A,B兩點間部分上的一個動點(不與點A,B重合),直線CD與y軸平行,交直線AB于點C,連接AD,BD.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com