
【題目】如圖,在![]() 中,AB為
中,AB為![]() 的直徑,C為
的直徑,C為![]() 上一點,P是
上一點,P是![]() 的中點,過點P作AC的垂線,交AC的延長線于點D.
的中點,過點P作AC的垂線,交AC的延長線于點D.
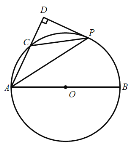
(1)求證:DP是![]() 的切線;
的切線;
(2)若AC=5,![]() ,求AP的長.
,求AP的長.
【答案】(1)見解析;(2)AP=![]() .
.
【解析】
(1)根據題意連接OP,直接利用切線的定理進行分析證明即可;
(2)根據題意連接BC,交于OP于點G,利用三角函數和勾股定理以及矩形的性質進行綜合分析計算即可.
解:(1)證明:連接OP;
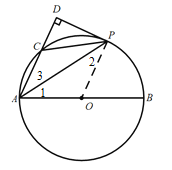
∵OP=OA;
∴∠1=∠2;
又∵P為![]() D的中點;
D的中點;
∴![]()
∴∠1=∠3;
∴∠3=∠2;
∴OP∥DA;
∵∠D=90°;
∴∠OPD=90°;
又∵OP為O半徑;
∴DP為O的切線;
(2)連接BC,交于OP于點G;
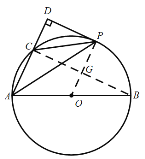
∵AB是圓O的直徑;
∴∠ACB為直角;
∵![]()
∴sin∠ABC=![]()
AC=5,則AB=13,半徑為![]()
由勾股定理的BC=![]() ,那么CG=6
,那么CG=6
又∵四邊形DCGP為矩形;
∴GP=DC=6.5-2.5=4
∴AD=5+4=9;
在Rt△ADP中,AP=![]() .
.


科目:初中數學 來源: 題型:
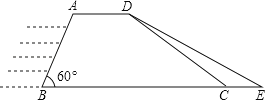
【題目】如圖,馬邊水務部門為加強馬邊河防汛工作,決定對某水電站水庫進行加固.原大壩的橫斷面是梯形ABCD,如圖所示,已知迎水面AB的長為10米,∠B=60°,背水面DC的長度為10![]() 米,加固后大壩的橫斷面為梯形ABED.若CE的長為4米.
米,加固后大壩的橫斷面為梯形ABED.若CE的長為4米.
(1)已知需加固的大壩長為120米,求需要填方多少立方米;
(2)求新大壩背水面DE的坡度.(計算結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在直角三角形ABC中,∠ACB=90°,BC的垂直平分線交BC點D,交AB于點E,過點A作AF∥CE交直線DE于點F.
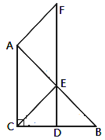
(1)求證:四邊形ACEF是平行四邊形;
(2)當∠B的大小滿足什么條件時,四邊形ACEF是菱形?請證明你的結論;
(3)四邊形ACEF有可能是矩形嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】發現與探索.

(1)根據小明的解答(圖1)分解因式(a-1)2-8(a-1)+7
(2)根據小麗的思考(圖2)解決問題,說明:代數式a2-12a+20的最小值為-16.
(3)求代數式-a2+12a-8的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,我們知道,若點![]() 將線段
將線段![]() 分成兩部分,且
分成兩部分,且![]() ,則稱點
,則稱點![]() 為線段
為線段![]() 的黃金分割點.類似的,我們把有一個內角等于
的黃金分割點.類似的,我們把有一個內角等于![]() 的等腰三角形稱為黃金三角形,如圖
的等腰三角形稱為黃金三角形,如圖![]() ,
,![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,
上,![]() ,過點
,過點![]() 作直線
作直線![]() 分別交直線
分別交直線![]() 和
和![]() 于點
于點![]() 、
、![]() ,連接
,連接![]() ,
,![]() .
.
(1)求![]() 的度數,并證明
的度數,并證明![]() 是黃金三角形;
是黃金三角形;
(2)求證:點![]() 是線段
是線段![]() 的黃金分割點;
的黃金分割點;
(3)對于實數:![]() ,如果滿足
,如果滿足![]() ,
,![]()
![]() 則稱
則稱![]() 為
為![]() ,
,![]() 的黃金數,
的黃金數,![]() 為
為![]() ,
,![]() 的白銀數.
的白銀數.
①實數![]() ,且
,且![]() 為
為![]() ,1的黃金數,
,1的黃金數,![]() 為
為![]() ,1的白銀數,求
,1的白銀數,求![]() 的值.
的值.
②實數![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,t的黃金數和白銀數,求
,t的黃金數和白銀數,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
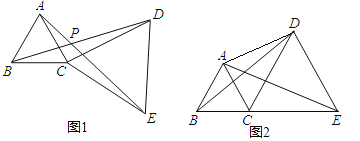
【題目】如圖1,△ABC和△DCE都是等邊三角形.
探究發現
(1)△BCD與△ACE是否全等?若全等,加以證明;若不全等,請說明理由.
拓展運用
(2)若B、C、E三點不在一條直線上,∠ADC=30°,AD=3,CD=2,求BD的長.
(3)若B、C、E三點在一條直線上(如圖2),且△ABC和△DCE的邊長分別為1和2,求△ACD的面積及AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A的坐標是A(x,y),從1、2、3這三個數中任取一個數作為x的值,再從余下的兩個數中任取一個數作為y的值.則點A落在直線y=﹣x+5與直線y=![]() x及y軸所圍成的封閉區域內(含邊界)的概率是_____.
x及y軸所圍成的封閉區域內(含邊界)的概率是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用四塊大正方形地磚和一塊小正方形地磚拼成如圖所示的實線圖案,每塊大正方形地磚面積為a,小正方形地磚面積為依次連接四塊大正方形地磚的中心得到正方形ABCD.則正方形ABCD的面積為____________(用含a,b的代數式表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果商計劃購進甲、乙兩種水果進行銷售,經了解,甲種水果的進價比乙種水果的進價每千克少4元,且用800元購進甲種水果的數量與用1000元購進乙種水果的數量相同.
(1)求甲、乙兩種水果的單價分別是多少元?
(2)該水果商根據該水果店平常的銷售情況確定,購進兩種水果共200千克,其中甲種水果的數量不超過乙種水果數量的3倍,且購買資金不超過3420元,購回后,水果商決定甲種水果的銷售價定為每千克20元,乙種水果的銷售價定為每千克25元,則水果商應如何進貨,才能獲得最大利潤,最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com