
【題目】在正方形ABCD中,過點A引射線AH,交邊CD于點H(點H與點D不重合).通過翻折,使點B落在射線AH上的點G處,折痕AE交BC于E,延長EG交CD于F.
(感知)(1)如圖①,當點H與點C重合時,猜想FG與FD的數量關系,并說明理由.
(探究)(2)如圖②,當點H為邊CD上任意一點時,(1)中結論是否仍然成立?請說明理由.
(應用)(3)在圖②中,當DF=3,CE=5時,直接利用探究的結論,求AB的長.

【答案】[感知] FG=FD,理由見解析;
[探究]成立,理由見解析;
[應用]![]() .
.
【解析】
[感知]運用折疊的性質可證明△AGF≌△ADF,從而得到FG=FD;
[探究] 運用折疊的性質可證明△AGF≌△ADF,從而得到FG=FD;
[應用] 由[探究]中的結論,可設AB=x,則FC=x-3,FE=x,然后在Rt△ECF中,根據勾股定理求解即可.
[感知]猜想:FG=FD.
證明:如圖所示:
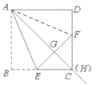 連接AF,
連接AF,
由折疊的性質可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
![]() ,
,
∴△AGF≌△ADF,
故可得FG=FD;
[探究] 當點H為邊CD上任意一點時,(1)中結論仍然成立.
證明:如圖所示:
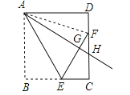 連接AF,
連接AF,
由折疊的性質可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
![]() ,
,
∴△AGF≌△ADF.
∴FG=FD,
故當點H為邊CD上任意一點時,(1)中的結論仍然成立;
[應用]設AB=x,則FC=x-3,FE=x,
在Rt△ECF中,EF2=FC2+EC2,即x2=(x-3)2+52,
解得x=![]() .
.
即AB的長為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點O,過點O作EF∥BC交AB于E,交AC于F,過點O作OD⊥AC于D,下列四個結論:
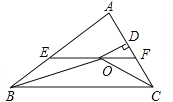
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③點O到△ABC各邊的距離相等;
④設OD=m,AE+AF=n,則![]() .
.
其中正確的結論是____.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,a∥b,則∠1+∠2=
(2)如圖2,AB∥CD,則∠1+∠2+∠3= ,并說明理由
(3)如圖3,a∥b,則∠1+∠2+∠3+∠4=
(4)如圖4,a∥b,根據以上結論,試探究∠1+∠2+∠3+∠4+…+∠n= (直接寫出你的結論,無需說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,E、F分別在AD、BC邊上,且AE=CF.
求證:(1)△ABE≌△CDF;
(2)四邊形BFDE是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD是△ABC的角平分線,點E,F分別在BC,AB上,且DE∥AB,BE=AF.
(1)求證:四邊形ADEF是平行四邊形;
(2)若∠ABC=60°,BD=4,求平行四邊形ADEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C為AB上一點,作CD⊥AB交⊙O于D,連接AD,將△ACD沿AD翻折至△AC′D.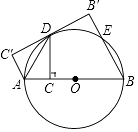
(1)請你判斷C′D與⊙O的位置關系,并說明理由;
(2)過點B作BB′⊥C′D′于B′,交⊙O于E,若CD= ![]() ,AC=3,求BE的長.
,AC=3,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】旋轉變換是解決數學問題中一種重要的思想方法,通過旋轉變換可以將分散的條件集中到一起,從而方便解決問題.已知,![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 在邊
在邊![]() 上,且
上,且![]() .
.

(1)如圖![]() ,當
,當![]() 時,將
時,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 到
到![]() 的位置,連接
的位置,連接![]() ,
,
①求![]() 的度數;
的度數;
②求證:![]() ;
;
(2)如圖![]() ,當
,當![]() 時,猜想
時,猜想![]() 、
、![]() 、
、![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
(3)如圖![]() ,當
,當![]() ,
,![]() ,
,![]() 時,請直接寫出
時,請直接寫出![]() 的長為________.
的長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在菱形ABCD中,∠ABC=60°,E是對角線AC上一點,F是線段BC延長線上一點,且CF=AE,連接BE、EF.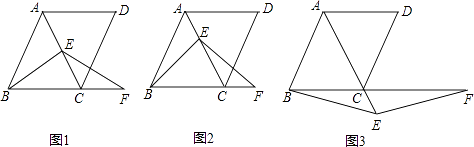
(1)若E是線段AC的中點,如圖1,易證:BE=EF(不需證明);
(2)若E是線段AC或AC延長線上的任意一點,其它條件不變,如圖2、圖3,線段BE、EF有怎樣的數量關系,直接寫出你的猜想;并選擇一種情況給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數 ![]() 的圖象經過坐標原點,與x軸的另一個交點為A(-2,0).
的圖象經過坐標原點,與x軸的另一個交點為A(-2,0).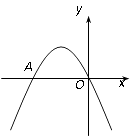
(1)求二次函數的解析式
(2)在拋物線上是否存在一點P,使△AOP的面積為3,若存在請求出點P的坐標,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com