
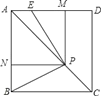
【題目】如圖,已知正方形ABCD的邊長為1,P是對角線AC上任意一點,E為AD上的點,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求證:四邊形PMAN是正方形;
(2)求證:EM=BN;
(3)若點P在線段AC上移動,其他不變,設PC=x,AE=y,求y關于x的解析式,并寫出自變量x的取值范圍.
【答案】(1)見解析;(2)見解析;(3)y=1-![]() (0≤x≤
(0≤x≤![]() ).
).
【解析】
(1)由四邊形ABCD是正方形,易得∠BAD=90°,AC平分∠BAD,又由PM⊥AD,PN⊥AB,即可證得四邊形PMAN是正方形;
(2)由四邊形PMAN是正方形,易證得△EPM≌△BPN,即可證得:EM=BN;
(3)首先過P作PF⊥BC于F,易得△PCF是等腰直角三角形,繼而證得△APM是等腰直角三角形,可得AP=![]() AM=
AM=![]() (AE+EM),繼而求得答案.
(AE+EM),繼而求得答案.
(1).∵正方形ABCD,
∴∠NAM=90.
又因為PM⊥AD,PN⊥AB,
∴∠ANP=∠AMP=90,
∴四邊形PMAN是矩形(有三個角是直角).
∵P在AC上,
∴PM=PN(角平分線上的點到這條線段兩邊的距離相等),
∴四邊形PMAN是正方形;
(2).∵∠EPB=90,
∴∠BPN+∠APN=90.
∵∠EPM=∠APN=90,
∴∠BPN=∠EPM,
在△BPN與△EPM中
∠BPN=∠EPM,PN=PM,∠BNP=∠EMP,
∴△BPN≌△EPM,
∴BN=EM;
(3)過P作PF⊥BC于F,如圖所示:
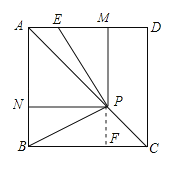
∵四邊形ABCD是正方形,
∴∠ABC=90°,AB=BC=1,∠PCF=45°,
∴AC=![]() ,△PCF是等腰直角三角形,
,△PCF是等腰直角三角形,
∴AP=AC-PC=![]() -x,BN=PF=
-x,BN=PF=![]() ,
,
∴EM=BN=![]() ,
,
∵∠PAM=45°,∠PMA=90°,
∴△APM是等腰直角三角形,
∴AP=![]() AM=
AM=![]() (AE+EM),
(AE+EM),
即![]() -x=
-x=![]() (y+
(y+![]() ),
),
解得:y=1-![]() x,
x,
∴x的取值范圍為0≤x≤![]() ,
,
∴y=1-![]() x(0≤x≤
x(0≤x≤![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是面積為4![]() 的等邊三角形,△ABC∽△ADE,
的等邊三角形,△ABC∽△ADE,
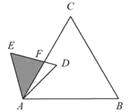
AB=2AD,∠BAD=45°,AC與DE相交于點F,則△AEF的面積
等于___(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《如果想毀掉一個孩子,就給他一部手機!》這是2017年微信圈一篇熱傳的文章.國際上,法國教育部宣布從 2018 年9月新學期起小學和初中禁止學生使用手機.為了解學生手機使用情況,某學校開展了“手機伴我健康行”主題活動,他們隨機抽取部分學生進行“使用手機目的”和“每周使用手機的時間”的問卷調查,并繪制成如圖①,②的 統計圖,已知“查資料”的人數是 40人.請你根據以上信息解答下列問題:
(1)在扇形統計圖中,“玩游戲”對應的百分比為______,圓心角度數是______度;
(2)補全條形統計圖;
(3)該校共有學生2100人,估計每周使用手機時間在2 小時以上(不含2小時)的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=![]() x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.
x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】過點A0,2的直線l1:y1kxbk0與直線l2:y2x1交于點P2,m。
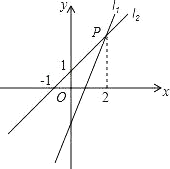
(1)求點P的坐標和直線l1的解析式;
(2)直接寫出使得y1y2的x的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于點Pa,b和點Qa,b,給出如下定義:若![]() ,則稱點Q為點P的限變點,例如:點(2,3)的限變點的坐標是(2,3),點2,5的限變點的坐標是2,5。
,則稱點Q為點P的限變點,例如:點(2,3)的限變點的坐標是(2,3),點2,5的限變點的坐標是2,5。
(1)在點A2,1,B1,2中有一個點是函數y=![]() 圖象上某一個點的限變點,這個點是 ;
圖象上某一個點的限變點,這個點是 ;
(2)求點![]() ,1的限變點的坐標;
,1的限變點的坐標;
(3)若點P在函數yx32xk,k2的圖象上,其限變點Q的縱坐標b的取值范圍是5b2,求k的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面給出四個結論:①BE=CF;②AB=DC;③
,下面給出四個結論:①BE=CF;②AB=DC;③![]() ;
;
④四邊形ABCD是矩形.其中說法正確的有( )
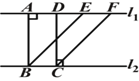
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com