
【題目】實驗證明,平面鏡反射光線的規律是:射到平面鏡上的光線和被反射出的光線與平面鏡所夾的銳角相等. 如圖1,一束光線m射到平面鏡a上,被a反射后的光線為n,則入射光線m、反射光線n與平面鏡a所夾的銳角∠1=∠2.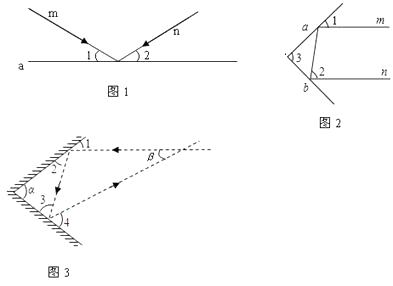
(1)如圖2,一束光線m射到平面鏡a上,被a反射到平面鏡b上,又被b反射.若被b反射出的光線n與光線m平行,且∠1=50°,則∠2=°,∠3=°.
(2)在(1)中m∥n,若∠1=55°,則∠3=°;若∠1=40°,則∠3=°.
(3)由(1)、(2),請你猜想:當兩平面鏡a、b的夾角∠3=°時,可以使任何射到平面鏡a上的光線m,經過平面鏡a、b的兩次反射后,入射光線m與反射光線n平行.你能說明理由嗎?
(4)如圖3,兩面鏡子的夾角為α°(0<α<90)時,進入光線與離開光線的夾角為β°
(0<β<90).試探索α與β的數量關系.直接寫出答案.
【答案】
(1)100;90
(2)90;90
(3)90;當∠3=90°時,m∥n.理由如下:
∵∠3=90°,
∴∠4+∠6=90°,
∴2∠4+2∠6=180°,
∴∠2+∠5=180°,
∴m∥n.
(4)![]()
【解析】解:(1)∵∠1=∠4=50°,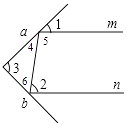
∴∠5=180°-2×50°=80°,
∵m∥n,
∴∠2+∠5=180°,
∴∠2=100°,
∴∠6= ![]() (180°-∠2)=40°,
(180°-∠2)=40°,
∴∠3=180°-∠4-∠6=90°;
(2)同樣的方法當∠1=55°,∠3=90°,∠1=40°, ∠3=90°
(3)當兩平面鏡a、b的夾角∠3=90°時,可以使任何射到平面鏡a上的光線m,經過平面鏡a、b的兩次反射后,入射光線m與反射光線n平行.
(4)如圖,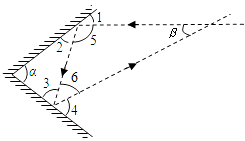
有∠5=180°-2∠2,∠6=180°-2∠3,
∵∠2+∠3=180°-∠α,
∴∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α,
∴α與β的數量關系為:2α+β=180°,


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案科目:初中數學 來源: 題型:
【題目】為了了解業余射擊隊隊員的射擊成績,對某次射擊比賽中每一名隊員的平均成績(單位:環,環數為整數)進行了統計,分別繪制了如下統計表和頻率分布直方圖,請你根據統計表和頻率分布直方圖回答下列問題: 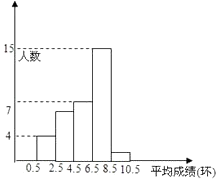
平均成績 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人數 | 0 | 1 | 3 | 3 | 4 | 6 | 1 | 0 |
(1)參加這次射擊比賽的隊員有多少名?
(2)這次射擊比賽平均成績的中位數落在頻率分布直方圖的哪個小組內?
(3)這次射擊比賽平均成績的眾數落在頻率分布直方圖的哪個小組內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設直線nx+(n+1)y= ![]() (n為自然數)與兩坐標軸圍成的三角形面積為Sn(n=1,2,…2014),則S1+S2+…+S2014的值為 .
(n為自然數)與兩坐標軸圍成的三角形面積為Sn(n=1,2,…2014),則S1+S2+…+S2014的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,將點A(﹣2,3)向右平移a個單位長度,再向下平移b個單位長度,平移后對應的點為A′,且點A和A′關于原點對稱,則a+b=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
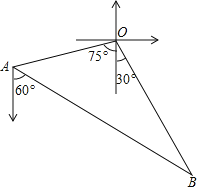
【題目】如圖,甲、乙兩漁船同時從港口O出發外出捕魚,乙沿南偏東30°方向以每小時15海里的速度航行,甲沿南偏西75°方向以每小時15![]() 海里的速度航行,當航行1小時后,甲在A處發現自己的漁具掉在乙船上,于是迅速改變航向和速度,仍以勻速沿南偏東60°方向追趕乙船,正好在B處追上.甲船追趕乙船的速度為多少海里/小時?
海里的速度航行,當航行1小時后,甲在A處發現自己的漁具掉在乙船上,于是迅速改變航向和速度,仍以勻速沿南偏東60°方向追趕乙船,正好在B處追上.甲船追趕乙船的速度為多少海里/小時?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:四邊形ABCD為平行四邊形,延長AD至E,使DE=AD,連接EB,EC,DB.添加一個條件,不能使四邊形DBCE為矩形的是( )

A. AB=BE B. BE⊥CD C. ∠ADB=900 D. CE⊥DE
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com